Dalam pelajaran matematika, kira-kira materi apa saja yang dipelajari di kelas 6 ya? Nah, sebagai bahan belajar siswa di rumah, berikut akan diberikan rangkuman materi matematika kelas 6 SD.
Matematika merupakan salah satu pelajaran yang diajarkan sejak SD. Untuk itu, setiap siswa wajib memahami materinya dengan baik.
Dengan memahami tiap-tiap pokok pembahasannya, akan memudahkan dalam mempelajari rumus yang berkaitan dengan materi matematika.
Rangkuman Materi Matematika Kelas 6 SD
Beberapa materi penting yang dipelajari di kelas 6 SD antara lain:
1. Perkalian Pecahan
Untuk menghitung perkalian pecahan, kalikan pembilang dengan pembilang, serta penyebut dengan penyebut.
Rumus menghitung perkalian pecahan adalah:
a/b x c/d = (a x c) / (b x d)
Contoh
1/2 x 3/4 = (1 x 3) / (2 x 4) = 3/8.
2 Pembagian Pecahan
Untuk menghitung pembagian pecahan, balikan posisi pembilang sebagai penyebut pada bilangan pembagi, kemudian ubah operasi pembagian menjadi perklaian.
Rumus menghitung pembagian pecahan adalah:
a/b x c/d = a/b x c/d
Contoh
1/2 : 3/4 = 1/2 x 4/3 = (1 x 4) / (2 x 3) = 4/6.
3. Perhitungan Desimal Dengan Pecahan Biasa
Diantara perhitungan desimal dengan pecahan biasa antara lain:
a. Mengubah Desimal Menjadi Pecahan
Untuk mengubah pecahan desimal menjadi pacahan biasa, caranya adalah:
- Jika terdapat 1 angka di belakang koma, ubahlah menjadi per sepuluh
- Jika terdapat 2 angka di belakang koma, ubahlah menjadi per seratus
- Jika terdapat 3 angka di belakang koma, ubahlah menjadi perseribu, dan seterusnya
Contoh
0,5 = …..
Karena terdapat 1 angka di belakang koma, maka diubah menjadi per sepuluh
0,5 = 5/10 = 1/2.
0,45 = …..
Karena terdapat 2 angka di belakang koma, maka diubah menjadi per seratus
0,45 = 45/100 = 9/20.
b. Menghitung Penjumlahan Desimal
Penjumlahan desimal dapat dihitung dengan langkah-langkah sebagai berikut:
- Meluruskan tanda koma
- Jumlahkan secara bersusun
Contoh
23,21 + 2,546 = 25,756.
c. Menghitung Pengurangan Desimal
Penguragan desimal dapat dihitung dengan langkah-langkah sebagai berikut:
- Meluruskan tanda koma
- Melakukan pengurangan secara bersusun
Contoh
9,421 – 2,31 = 7,111.
d. Menghitung Perkalian Desimal
Untuk menghitung perkalian desimal, langkah-langkahnya adalah:
- Menghitung jumlah angka yang berada di belakang koma
- Menghilangkan tanda koma
- Mengalikan bilangan bulat
- Mengembalikan tanda koma sesuai jumlah yang dihilangkan
Contoh
1,25 x 1,5 = …..
125 x 15 = 1875 = 1,875.
e. Menghitung Pembagian Desimal
Untuk menghitung pembagian desimal, langkah-langkahnya adalah:
- Ubah desimal menjadi pecahan
- Menghitung pembagian pecahan
- Ubah hasilnya menjadi desimal
Contoh
2,1 : 0,5 = …..
2,1 = 21/10
0,5 = 5/10
21/10 : 5/10 = 21/10 x 10/5 = 210/50 = 42/10 = 4,2.
4. Luas Bangun Datar
Rumus untuk menghitung luas bangun datar adalah:
| Persegi | L = s x s |
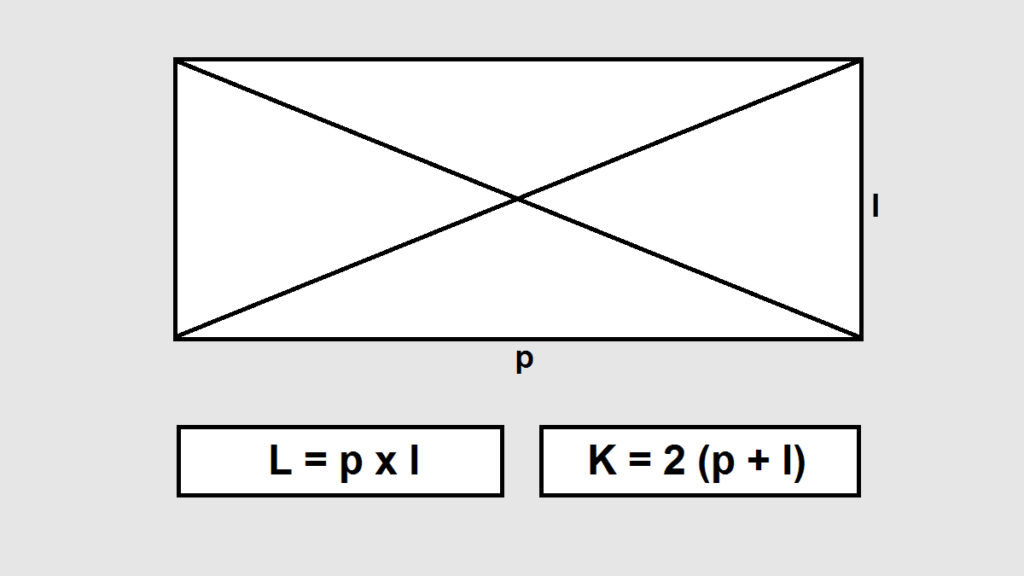
| Persegi panjang | L = p x l |
| Segitiga | L = 1/2 x a x t |
| Trapesium | L = 1/2 x (a + b) x t |
| Jajar genjang | L = a x t |
| Belah ketupat | L = 1/2 x d1 x d2 |
| Layang-layang | L = 1/2 x d1 x d2 |
| Lingkaran | L = π x r² |
Contoh
1. Persegi memiliki ukuran sisi 10 cm. Berapakah luas persegi?
L = sisi x sisi
L = 10 x 10
L = 100 cm².
2. Persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Berapakah luas persegi panjang?
L = panjang x lebar
L = 12 x 8
L = 96 cm².
3. Segitiga memiliki ukuran alas 8 cm dan tinggi 6 cm. Berapakah luas segitiga?
L = 1/2 x a x t
L = 1/2 x 8 x 6
L = 24 cm².
4. Trapesium memiliki ukuran pada sisi sejajarnya 10 cm dan 12 cm, serta tingginya 7 cm. Berapakah luas trapesium?
L = 1/2 x (a + b) x t
L = 1/2 x (10 + 12) x 7
L = 1/2 x 22 x 7
L = 77 cm².
5. Jajar genjang memiliki ukuran sisi alas 11 cm dan tinggi 9 cm. Berapakah luas jajar genjang?
L = a x t
L = 11 x 9
L = 99 cm².
6. Belah ketupat memiliki panjang diagonal 12 cm dan 13 cm. Berapakah luas belah ketupat?
L = 1/2 x d1 x d2
L = 1/2 x 12 x 13
L = 78 cm².
7. Layang-layang memiliki panjang diagonal 15 cm dan 18 cm. Berapakah luas layang-layang?
L = 1/2 x d1 x d2
L = 1/2 x 15 x 18
L = 135 cm².
8. Lingkaran memiliki jari-jari 7 cm. Berapakah luas lingkaran?
L = π x r²
L = 22/7 x 7²
L = 22/7 x 49
L = 154 cm².
5. Volume Bangun Ruang
Rumus untuk menghitung volume bangun ruang adalah:
| Kubus | V = s x s x s |
| Balok | V = p x l x t |
| Prisma | V = La x t |
| Limas | V = 1/3 x La x t |
| Kerucut | V = 1/3 x π x r² x t |
| Tabung | V = π x r² x t |
| Bola | V = 4/3 x π x r³ |
Contoh
1. Kubus memiliki panjang rusuk 5 cm. Berapakah volumenya?
V = s x s x s
V = 5 x 5 x 5
V = 125 cm³.
2. Balok memiliki ukuran panjang 10 cm, lebar 8 cm, dan tinggi 6 cm. Berapakah volumenya?
V = p x l x t
V = 10 x 8 x 6
V = 480 cm³.
3. Prisma memiliki sisi alas luas alas 100 cm² dan tinggi 7 cm. Berapakah volumenya?
V = La x t
V = 100 x 7
V = 700 cm³.
4. Limas memiliki luas alas 48 cm² dan tinggi 9 cm. Berapakah volumenya?
V = 1/3 x La x t
V = 1/3 x 48 x 9
V = 144 cm³.
5. Kerucut memiliki jari-jari alas 7 cm dan tinggi 15 cm. Berapakah volumenya?
V = 1/3 x π x r² x t
V = 1/3 x 22/7 x 7² x 15
V = 1/3 x 22/7 x 49 x 15
V = 770 cm³.
6. Tabung memiliki jari-jari 7 cm dan tinggi 6 cm. Berapakah volumenya?
V = π x r² x t
V = 22/7 x 7² x 6
V = 22/7 x 49 x 6
V = 924 cm³.
7. Sebuah bola memiliki jari-jari 7 cm. Berapakah volumenya?
V = 4/3 x π x r³
V = 4/3 x 22/7 x 7³
V = 4/3 x 22/7 x 343
V = 1.437,33 cm³.
6. Kecepatan
Rumus untuk menghitung kecepatan adalah:
| V = s : t |
Keterangan:
V = kecepatan (km/jam)
S = jarak (km)
t = waktu (jam)
Contoh
Ayah pergi dari kota A ke kota B menempuh perjalanan selama 2 jam. Jika jarak dari kota A ke kota B adalah 100 km, berapakah kecepatan ayah dalam menempuh perjalanan?
V = s : t
V = 100 : 2
V = 50 km/jam.
Demikianlah pembahasan mengenai rangkuman materi matematika kelas 6 SD. Semoga bermanfaat.