Bangun Ruang: Jenis, Gambar, Ciri-Ciri, Rumus, Dan Contoh Soal

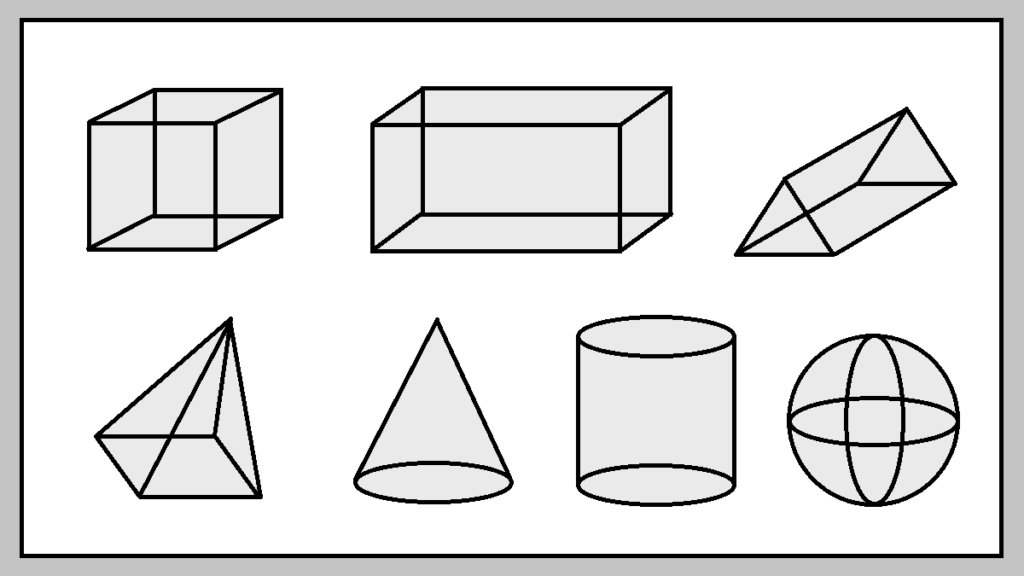
Dalam pelajaran matematika, terdapat materi bangun ruang. Materi bangun ruang sangat penting untuk dipahami. Hal ini mengingat terdapat berbagai jenis, ciri-ciri, dan rumus bangun ruang yang berbeda-beda.

A. Pengertian Bangun Ruang

Bangun ruang adalah bangun tiga dimensi yang memiliki volume atau isi. Yang termasuk jenis-jenis bangun ruang dalam matematika antara lain kubus, balok, limas, prisma, kerucut, tabung, dan bola.

Setiap bangun ruang memiliki ciri-ciri yang berbeda. Begitu juga dengan unsur-unsur pembentuknya seperti sisi, rusuk, dan titik sudut yang jumlahnya mengikuti bentuk ruangannya.

Bentuk bangun ruang sering diterapkan di kehidupan sehari-hari. Berikut merupakan contoh benda yang menerapkan bentuk bangun ruang, diantaranya yaitu:

Dadu, rubik merupakan contoh benda berbentuk kubus
Lemari, kotak kardus merupakan contoh benda berbentuk balok
Piramida merupakan contoh benda berbentuk limas
Coklat toblerone adalah contoh benda berbentuk prisma segitiga
Es krim cone, nasi tumpeng merupakan contoh benda berbentuk kerucut
Kaleng susu, drum merupakan contoh bentuk berbentuk tabung
Kelereng, bola basket merupakan contoh benda berbentuk bangun bola

B. Jenis-Jenis Bangun Ruang

Secara umum, bangun dibedakan menjadi bangun ruang sisi datar dan bangun ruang sisi lengkung.

Yang termasuk bangun ruang sisi datar yaitu kubus, balok, limas, dan prsima. Sedangkan bangun ruang sisi lengkung terdiri dari tabung, kerucut, dan bola.

Berikut merupakan jenis-jenis bangun ruang beserta gambar dan ciri-cirinya.

1. Kubus

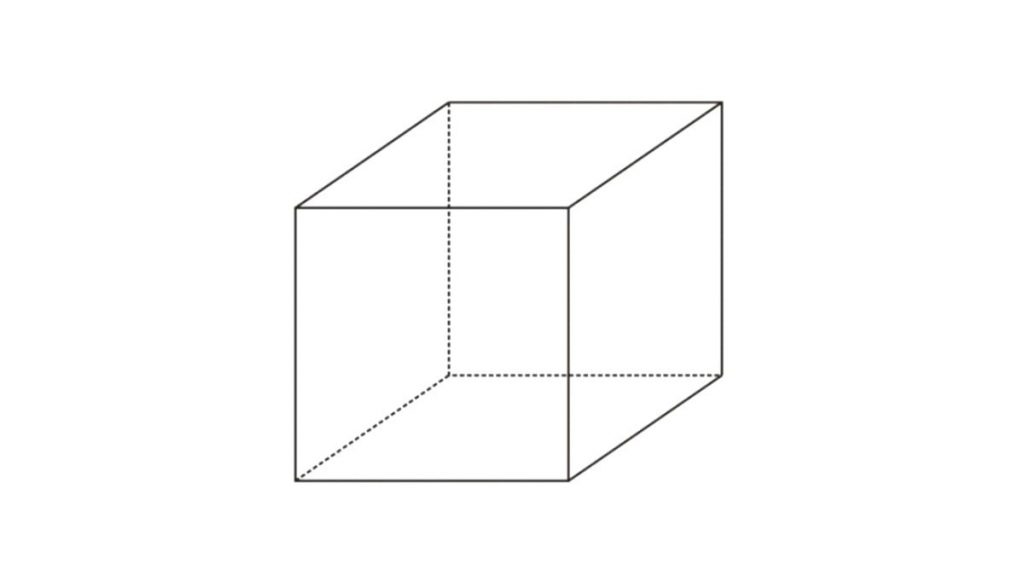
Kubus adalah bangun ruang yang dibatasi oleh enam sisi berbentuk persegi sama besar.

Ciri-ciri kubus adalah:

Memiliki 6 sisi
Memiliki 12 rusuk
Memiliki 8 titik sudut
Memiliki 12 diagonal bidang
Memiliki 4 diagonal ruang
Memiliki 6 bidang diagonal

Baca Lainnya : Rumus Luas Permukaan Prisma Segitiga Dan Contoh Soalnya

2. Balok

Balok adalah bangun ruang yang dibatasi oleh enam sisi berbentuk persegi dan persegi panjang, dimana setiap pasangan sisi yang berhadapan berukuran sama besar.

Ciri-ciri balok adalah:

Memiliki 6 sisi
Memiliki 12 rusuk
Memiliki 8 titik sudut
Memiliki 12 diagonal bidang
Memiliki 4 diagonal ruang
Memiliki 6 bidang diagonal

3. Limas

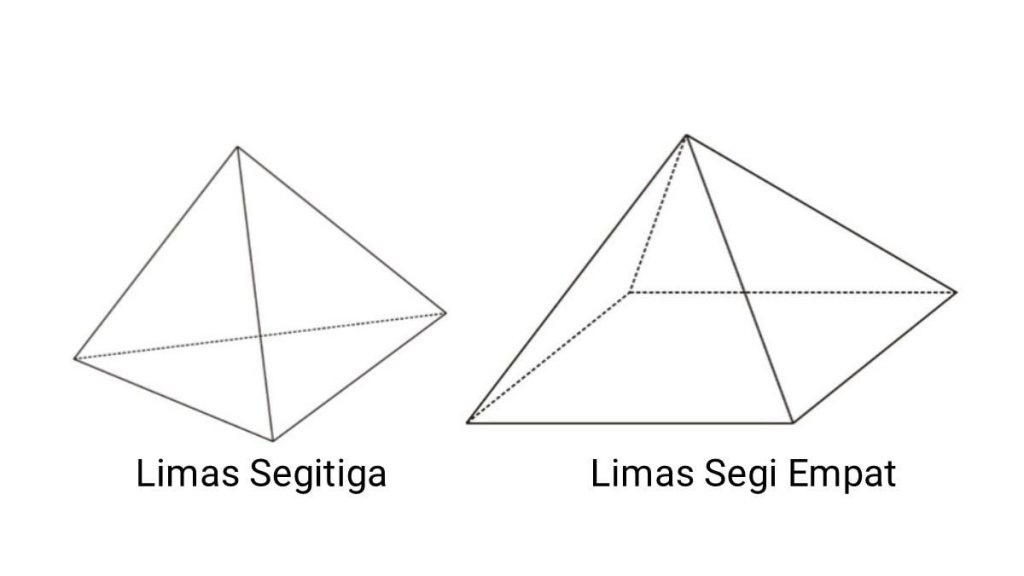
Limas adalah bangun ruang yang dibatasi oleh sisi alas berbentuk segi-n dan sisi tegak berbentuk segitiga.

Bangun ruang limas memiliki beberapa jenis berdasarkan bentuk sisi alasnya. Diantaranya yaitu limas segitiga dan limas segi empat.

a. Limas Segitiga

Limas segitiga adalah jenis limas yang sisi alasnya berbentuk segitiga. Ciri-cirinya adalah:

Memiliki 4 sisi
Memiliki 6 rusuk
Memiliki 4 titik sudut

b. Segi Empat

Limas segi empat adalah jenis limas yang sisi alasnya berbentuk segi emapt. Ciri-cirinya adalah:

Memiliki 5 sisi
Memiliki 8 rusuk
Memiliki 5 titik sudut

4. Prisma

Prisma adalah bangun ruang yang dibatasi oleh sisi alas dan sisi atas berbentuk segi-n kongruen, serta sisi tegak berbentuk segi empat.

Sama halnya dengan limas, bangun ruang prisma memiliki beberapa jenis berdasarkan bentuk sisi alas dan sisi atasnya. Diantaranya yaitu prisma segitiga dan prisma segi empat.

a. Prisma Segitiga

Prisma segitiga adalah jenis prisma yang sisi alasnya berbentuk segitiga. Ciri-cirinya adalah:

Memiliki 5 sisi
Memiliki 9 rusuk
Memiliki 6 titik sudut
Memiliki 6 diagonal bidang
Tidak memiliki diagonal ruang
Tidak memiliki bidang diagonal

b. Prisma Segi Empat

Prisma segi empat adalah jenis prisma yang sisi alasnya berbentuk segi empat. Ciri-cirinya adalah:

Memiliki 6 sisi
Memiliki 12 rusuk
Memiliki 8 titik sudut
Memiliki 12 diagonal bidang
Memiliki 4 diagonal ruang
Memiliki 6 bidang diagonal

Baca Lainnya : Mengenal 10 Nama Bangun Datar Dua Dimensi

5. Tabung

Tabung adalah bangun ruang yang dibatasi oleh sisi alas dan sisi atas berbentuk lingkaran, serta sisi tegak berbentuk lengkungan persegi panjang.

Ciri-ciri tabung adalah:

Memiliki 3 sisi
Memiliki 2 rusuk
Tidak memiliki titik sudut

6. Kerucut

Kerucut adalah bangun ruang yang dibatasi oleh sisi alas berbentuk lingkaran dan sisi selimut yang berbentuk juring lingkaran.

Ciri-ciri kerucut adalah:

Memiliki 2 sisi
Memiliki 1 rusuk
Memiliki 1 titik puncak

7. Bola

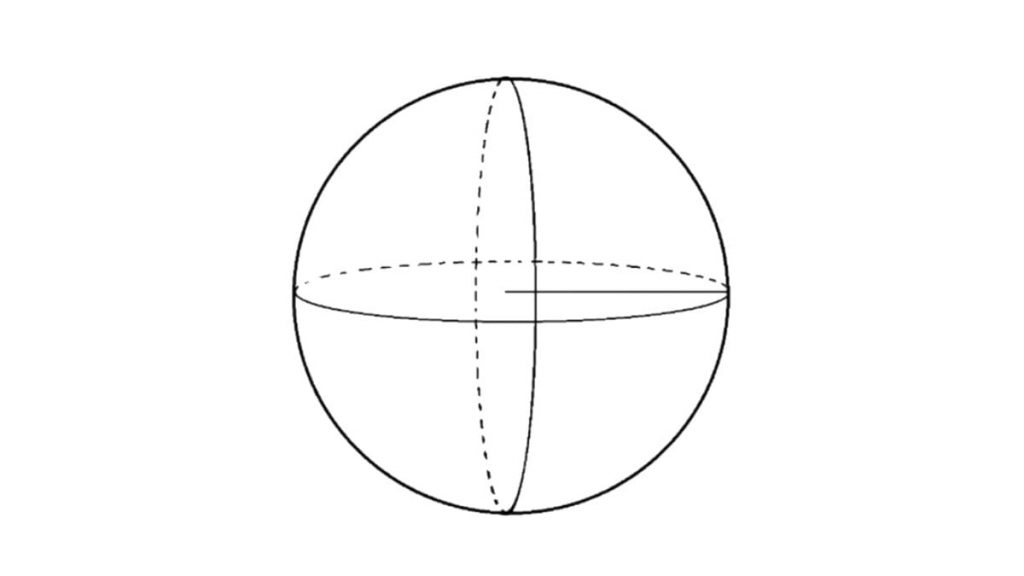
Bola adalah bangun ruang yang dibatasi oleh sebuah sisi berbentuk lengkung. Bola memiliki bentuk bulat sempurna.

Ciri-ciri bola adalah:

Memiliki 1 sisi
Tidak memiliki rusuk
Tidak memiliki titik sudut
Memiliki 1 titik pusat
Memiliki jari-jari
Memiliki diameter

Rumus Bangun Ruang

Perhitungan dasar bangun ruang adalah volume dan luas permukaan. Rumus yang digunakan untuk menghitung volume dan luas permukaan bangun ruang adalah:

Bangun Ruang	Volume	Luas Permukaan
Kubus	s x s x s	6 x s x s
Balok	p x l x t	2 ( p x l + p x t + l x t )
Limas	1/3 x luas alas x tinggi	luas alas + luas seluruh sisi tegak
Prisma	luas alas x tinggi	(2 x luas alas) + (keliling alas x tinggi)
Tabung	π x r² x t	2 x π x r x (r + t)
Kerucut	1/3 x π x r² x t	π x r (r + s)
Bola	4/3 x π x r³	4 x π x r²

Contoh Soal

1. Sebuah kubus memiliki panjang rusuk 10 cm. Berapa volume dan luas permukaan kubus tersebut?

Penyelesaian:
V = s x s x s
V = 10 x 10 x 10
V = 1.000 cm³

L = 6 x s x s
L = 6 x 10 x 10
L = 600 cm²

2. Sebuah balok memiliki ukuran panjang 10 cm, lebar 8 cm dan tinggi 5 cm. Berapa volume dan luas permukaan balok tersebut?

Penyelesaian:
V = p x l x t
V = 10 x 8 x 5
V = 400 cm³

L = 2 ( p x l + p x t + l x t )
L = 2 (10 x 8 + 10 x 5 + 8 x 5)
L = 2 (80 + 50 + 40)
L = 2 x 170
L = 340 cm²

3. Sebuah limas segitiga memiliki luas alas 60 cm² dan luas sisi tegak 30 cm². Jika tinggi limas 10 cm, berapa volume dan luas permukaan limas tersebut?

Baca Lainnya : Contoh Soal Luas Trapesium Dan Jawabannya

Penyelesaian:
V = 1/3 x luas alas x tinggi
V = 1/3 x 60 x 10
V = 1/3 x 600
V = 200 cm³

L = luas alas + luas seluruh sisi tegak
L = luas alas + (3 x luas sisi tegak)
L = 60 + (3 x 30)
L = 60 + 90
L = 150 cm²

4. Sebuah prisma persegi memiliki panjang sisi alas 10 cm dan tinggi prisma 15 cm. Berapa volume dan luas permukaan prisma tersebut?

Penyelesaian:
V = luas alas x tinggi
V = (sisi x sisi) x tinggi
V = (10 x 10) x 15
V = 100 x 15
V = 1.500 cm³

L = (2 x luas alas) + (keliling alas x tinggi)
L = (2 x s x s) + (4 x s x tinggi)
L = (2 x 10 x 10) + (4 x 10 x 15)
L = 200 + 600
L = 800 cm²

5. Perhatikan gambar di bawah ini dan tentukan berapa volume dan luas permukaan tabung tersebut!

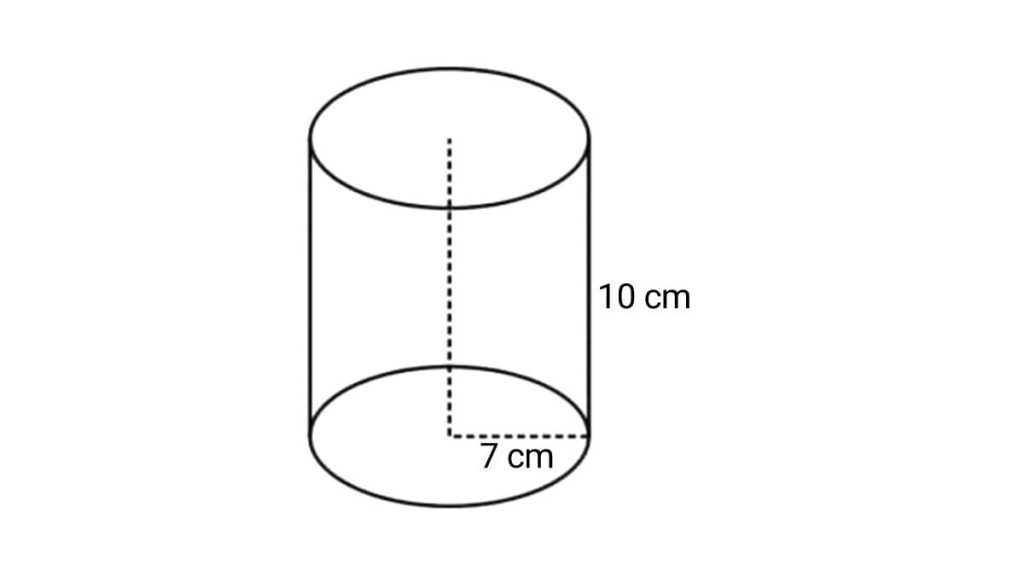
Penyelesaian:
V = π x r² x t
V = 22/7 x 7² x 10
V = 22/7 x 49 x 10
V = 154 x 10
V = 1.540 cm³

L = 2 x π x r x (r + t)
L = 2 x 22/7 x 7 x (7 + 10)
L = 44 x 17
L = 748 cm²

6. Sebuah kerucut memiliki sisi alas dengan jari-jari 7 cm dan tinggi 24 cm, berapa volume dan luas permukaan kerucut tersebut?

Penyelesaian:
V = 1/3 x π x r² x t
V = 1/3 x 22/7 x 7² x 24
V = 1/3 x 22/7 x 49 x 24
V = 1/3 x 3.696
V = 1.232 cm³

s² = r² + t²
s² = 7² + 24²
s² = 49 + 576
s² = 625
s = √625
s = 25 cm

L = π x r (r + s)
L = 22/7 x 7 (7 + 25)
L = 22 x 32
L = 704 cm²

7. Sebuah bola memiliki jari-jari 7 cm. Berapa volume dan luas permukaan bola tersebut?

Penyelesaian:
V = 4/3 x π x r³
V = 4/3 x 22/7 x 7³
V = 4/3 x 22/7 x 343
V = 4/3 x 1.078
V = 1.437,33 cm³

L = 4 x π x r²
L = 4 x 22/7 x 7²
L = 4 x 22/7 x 49
L = 4 x 154
L = 616 cm²

Demikanlah pembahasan mengenai mengenai pengertian, jenis-jenis, gambar, ciri-ciri, rumus, dan contoh soal bangun ruang. Semoga bermanfaat.

Baca Juga :