Cara Mencari Sudut Segitiga – Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Berdasarkan sudutnya, segitiga dibedakan menjadi segitiga lancip, segitiga tumpul, dan segitiga siku-siku.
Meskipun memiliki jenis-jenis yang berbeda, namun jika ketiga sudut segitiga dijumlahkan, besarya adalah 180°. Dari konsep ini, kita dapat mencari sudut segitiga yang belum diketahui diketahui.
Selain itu, jika terdapat dua sudut yang membentuk sudut lurus, maka jumlah kedua sudut tersebut adalah 180°. Konsep ini juga penting untuk menentukan sudut luar segitiga.
Cara Mencari Sudut Segitiga Dan Contoh Soal
Perhitungan sudut-sudut segitiga sering kali dipertanyakan. Untuk dapat menjawabnya, kita perlu memahami aturan-aturan sudut pada segitiga berikut ini:
- Perhatikan sudut yang telah diketahui
- Jika ketiga sudut segitiga dijumlahkan, besarnya adalah 180°
- Salah satu sudut segitiga siku-siku besarnya 90°
- Segitiga sama sisi mempunyai 3 sudut yang sama besar, yaitu 60°
- Segitiga sama kaki mempunyai 2 sudut yang sama besar
- Jika terdapat dua sudut yang membentuk sudut lurus, maka jumlahnya adalah 180°
Untuk memahami aturan-aturan tersebut, silahkan simak contoh soal berikut ini.
Contoh Soal 1
Perhatikan gambar segitiga di bawah ini dan tentukan besar sudut CAB!

Penyelesaian:
Jika ketiga sudut segitiga dijumlahkan, besarnya adalah 180°
∠ CAB + ∠ ABC + ∠ BCA = 180°
∠ CAB + 60° + 75° = 180°
∠ CAB + 135° = 180°
∠ CAB = 180° – 135°
∠ CAB = 45°
Jadi, besar sudut CAB adalah 45°.
Contoh Soal 2
Berapakah besar sudut ABC pada gambar segitiga di bawah ini?
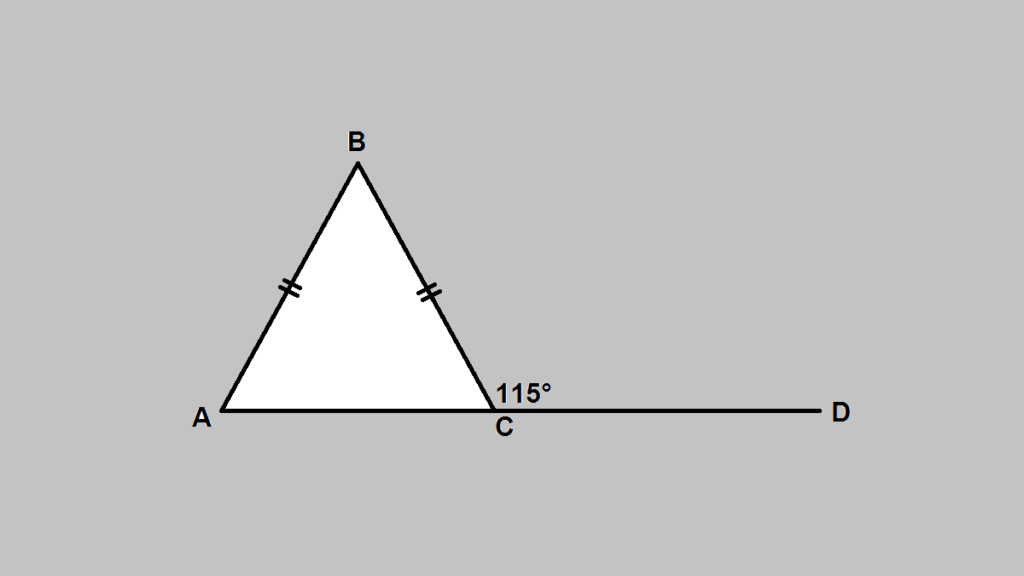
Penyelesaian:
Jika terdapat dua sudut yang membentuk sudut lurus, maka jumlahnya adalah 180°
∠ BCD + ∠ BCA = 180°
∠ 115° + ∠ BCA = 180°
∠ BCA = 180° – 115°
∠ BCA = 65°
Segitiga sama kaki mempunyai 2 sudut yang sama besar
∠ BCA = ∠ BAC = 65°
Jumlah ketiga sudut segitiga adalah 180°
∠ ABC + ∠ BCA + ∠ BAC = 180°
∠ ABC + 65° + 65° = 180°
∠ ABC + 130° = 180°
∠ ABC = 180° – 130°
∠ ABC = 50°
Jadi, besar sudut ABC adalah 50°.
Contoh Soal 3
Perhatikan gambar di bawah ini!

Tentukan sudut PQR!
Penyelesaian:
Salah satu sudut segitiga siku-siku besarnya 90°
sudut RPQ = sudut siku-siku = 90°
∠ PQR + ∠ QRP + ∠ RPQ = 180°
∠ PQR + 40° + 90° = 180°
∠ PQR + 130° = 180°
∠ PQR = 180° – 130°
∠ PQR = 50°
Jadi, besar sudut PQR adalah 50°.
Contoh Soal 4
Perhatikan gambar segitiga di bawah ini!

Berapakah besar sudut ABC?
Penyelesaian:
Jika terdapat dua sudut yang membentuk sudut lurus, maka jumlahnya adalah 180°
∠ DAC + ∠ CAB = 180°
∠ 120° + ∠ CAB = 180°
∠ CAB = 180° – 120°
∠ CAB = 60°
Segitiga sama sisi mempunyai 3 sudut yang sama besar
∠ CAB = ∠ ABC = ∠ BCA = 60°
Jadi, besar sudut ABC adalah 60°.
Contoh Soal 5
Perhatikan gambar segitiga di bawah ini!
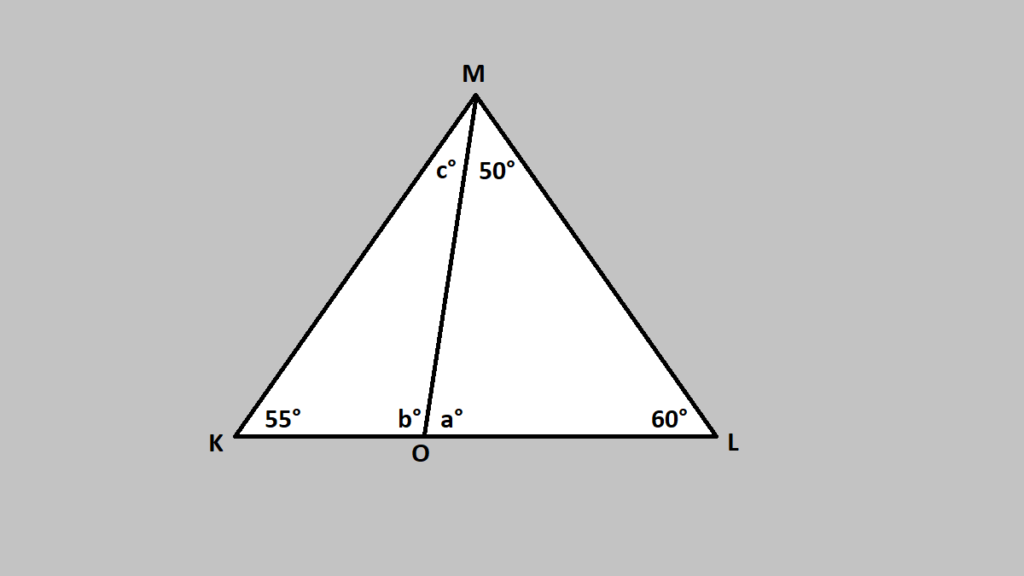
Tentukan!
a. Berapakah besar sudut a°
b. Berapakah besar sudut b°
c. Berapakah besar sudut c°
Penyelesaian:
a. Mencari besar sudut a
Jumlah ketiga sudut segitiga adalah 180°
∠ a + ∠ OLM + ∠ LMO = 180°
∠ a + 60° + 50° = 180°
∠ a + 110° = 180°
∠ a = 180° – 110°
∠ a = 70°
Jadi, besar sudut a = 70°.
b. Mencari besar sudut b
Jika terdapat dua sudut yang membentuk sudut lurus, maka jumlahnya adalah 180°
∠ a + ∠ b = 180°
∠ 70° + ∠ b = 180°
∠ b = 180° – 70°
∠ b = 110°
Jadi, besar sudut b = 70°.
c. Mencari besar sudut c
Jumlah ketiga sudut segitiga adalah 180°
∠ c + ∠ b + ∠ MKO = 180°
∠ c + 110° + 55° = 180°
∠ c + 165° = 180°
∠ c = 180° – 165°
∠ c = 15°
Jadi, besar sudut c = 15°.
Demikianlah pembahasan mengenai cara mencari sudut segitiga dan contoh soalnya. Semoga bermanfaat.
Baca Juga :
- Cara Menentukan Sudut Segitiga Sama Kaki
- Garis-Garis Istimewa Pada Segitiga Beserta Gambarnya
- Cara Mencari Sisi Segitiga Siku-Siku
- Jenis – Jenis Sudut Berdasarkan Nilainya
- Cara Menghitung Sudut Pusat Dan Sudut Keliling Lingkaran