Sudut Berpelurus, Berpenyiku, Dan Bertolak Belakang – Sudut adalah daerah yang terbentuk oleh dua garis yang saling berpotongan pada titik pangkalnya. Jika terdapat dua sudut saling dihubungkan, maka akan membentuk hubungan antar sudut.
Hubungan antar sudut dapat berupa sudut berpelurus, sudut berpenyiku, dan sudut bertolak belakang. Masing-masing hubungan tersebut memiliki rumus untuk menentukan pasangan sudutnya.
Nah, berikut akan dijelaskan apa itu hubungan antara sudut berpelurus, sudut berpenyiku, dan sudut bertolak belakang beserta rumus dan contoh soalnya.
Sudut Berpelurus

Dua buah sudut dikatakan berpelurus jika besar kedua sudut dijumlahkan, maka besarnya adalah 180°. Sudut berpelurus disebut juga dengan sudut bersuplemen.
Rumus Sudut Berpelurus
Rumus untuk menentukan sudut yang belum diketehui pada sudut berpelurus adalah:
| ∠ a + ∠ b = 180° |
| ∠ a = 180° – ∠ b |
| ∠ b = 180° – ∠ a |
Contoh Soal
Perhatikan gambar di bawah ini!

Tentukanlah!
a. Mana saja yang termasuk sudut berpelurus?
b. Jika besar ∠ aob = 60°, berapakah ∠ boc?
Penyelesaian:
a. Yang termasuk sudut berpelurus adalah:
- ∠ aob dengan ∠ boc
- ∠ boc dengan ∠ cod
- ∠ cod dengan ∠ doa
- ∠ doa dengan ∠ aob
b. Besar ∠ boc adalah:
- ∠ aob + ∠ boc = 180°
- ∠ boc = 180° – ∠ aob
- ∠ boc = 180° – 60°
- ∠ boc = 120°
Sudut Berpenyiku

Dua buah sudut dikatakan berpenyiku jika besar kedua sudut dijumlahkan, maka besarnya adalah 90°. Sudut berpenyiku disebut juga dengan sudut berkomplemen.
Rumus Sudut Berpenyiku
Rumus untuk menentukan sudut yang belum diketehui pada sudut berpenyiku adalah:
| ∠ a + ∠ b = 90° |
| ∠ a = 90° – ∠ b |
| ∠ b = 90° – ∠ a |
Contoh Soal
Perhatikan gambar di bawah ini!
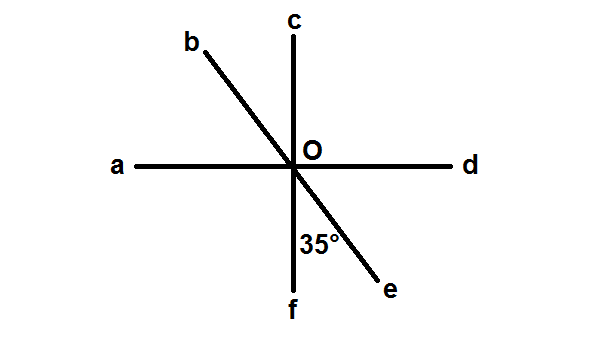
Tentukanlah!
a. Mana saja yang termasuk sudut berpeyiku?
b. Jika besar ∠ eof = 35°, berapakah ∠ doe?
Penyelesaian:
a. Yang termasuk sudut berpenyiku adalah:
- ∠ aob dengan ∠ boc
- ∠ doe dengan ∠ eof
b. Besar ∠ doe adalah:
- ∠ doe + ∠ eof = 90°
- ∠ doe = 90° – ∠ eof
- ∠ doe = 90° – 35°
- ∠ doe = 55°
Sudut Bertolak Belakang

Sudut saling bertolak belakang terbentuk dari dua buah garis yang saling berpotongan di tengahnya. Besar sudut yang saling bertolak belakang adalah sama.
Rumus Sudut Bertolak Belakang
Rumus untuk menentukan sudut yang belum diketahui pada sudut saling bertolak belakang adalah:
| ∠ a = ∠ b |
Contoh Soal
Perhatikan gambar di bawah ini!

Tentukanlah!
a. Mana saja yang termasuk sudut bertolak belakang?
b. Jika besar ∠ boc = 145°, berapakah ∠ aod?
Penyelesaian:
a. Yang termasuk sudut bertolak belakang adalah:
- ∠ aob dengan ∠ doc
- ∠ boc dengan ∠ aod
b. Besar sudut ∠ aod adalah:
- ∠ boc = ∠ aod
- ∠ boc = 145°
- ∠ aod = 145°
Demikianlah pembahasan mengenai hubungan antar dua sudut yang saling berpelurus, berpenyiku, dan bertolak belakang. Semoga bermanfaat.
Baca Juga :