Kedudukan Dua Garis – Pernahkah memperhatikan keramik lantai! Setiap pertemuan antar sisi keramik membentuk garis. Garis-garis tersebut memiliki kedudukan antara yang satu dengan lainnya.
Garis adalah unsur geometri paling sederhana yang terbentuk oleh himpunan titik-titik yang saling berhubungan. Garis hanya memiliki satu dimensi, yaitu panjang.
Dalam matematika, dua buah garis pada bidang datar dapat memiliki beberapa kedudukan. Kedudukan dua garis tersebut adalah sejajar, berpotongan, berimpit, bersilangan, dan vertikal horizontal.
Kedudukan Dua Garis Beserta Contoh Gambarnya
1. Kedudukan Garis Sejajar
Dua garis dikatakan sejajar apabila kedua garis tersebut terletak pada satu bidang datar dan tidak akan pernah berpotongan meskipun garis tersebut diperpanjang sampai tak terhingga.
Garis yang saling sejajar disimbolkan dengan tanda ̸ ̸ . Secara umum, sifat-sifat kedudukan garis sejajar adalah:
- Jika suatu garis memotong salah satu dari dua garis yang sejajar, maka garis tersebut juga akan memotong garis lainnya
- Jika sebuah garis sejajar dengan dua buah garis, maka ketiga garis tersebut saling sejajar
- Jika terdapat sebuah titik di luar garis, maka hanya terdapat satu garis yang sejajar dengan garis tersebut yang melalui titi
2. Kedudukan Garis Berpotongan
Dua garis dikatakan saling berpotongan apabila kedua garis tersebut terletak pada satu bidang datar dan berpotongan di salah satu titiknya.
3. Kedudukan Garis Berimpit
Dua garis dikatakan saling berimpit apabila kedua garis tersebut terletak pada satu garis lurus dan memiliki lebih dari dua titik potong. Sehingga dua garis yang berimpit akan saling menutupi dan terlihat seperti satu garis.
4. Kedudukan Garis Bersilangan
Dua garis dikatakan bersilangan apabila kedua garis tersebut tidak terletak pada satu bidang datar dan tidak akan berpotongan meskipun diperpanjang secara terus menerus.
5. Kedudukan Garis Vertikal Horizontal
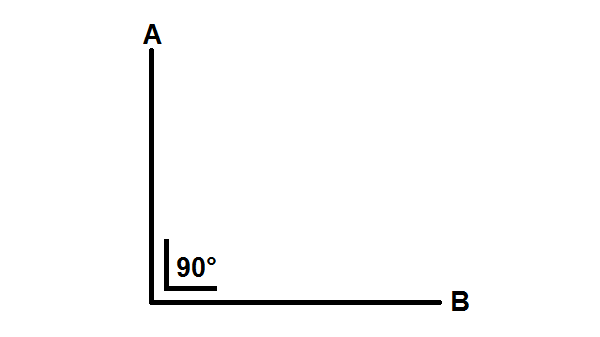
Dua garis dikatakan saling vertikal horizontal apabila kedua garis tersebut terletak pada satu bidang datar dan saling berpotongan tegak lurus membentuk sudut 90°.
Demikianlah pembahasan mengenai kedudukan dua garis pada bidang datar dan contoh gambarnya. Semoga bermanfaat.
Baca Juga :
