Kedudukan Titik, Garis, Dan Bidang – Dalam geometri tiga dimensi, terdapat istilah titik, garis, dan bidang. Ketiga unsur tersebut dapat memiliki kedudukan antar yang satu dengan lainnya.
Titik, Garis, Dan Bidang
Titik adalah objek terkecil pada geometri karena tidak memiliki ukuran, baik panjang, lebar, maupun luas. Penulisan titik disimbolkan dengan noktah (.) dan penamaannya menggunakan huruf kapital. Contohnya . A, . B, . C, dan lainnya.
Garis adalah himpunan titik-titik yang beraturan dan mempunyai ukuran panjang tak terbatas. Penamaan garis biasanya mengambil dari simbol yang terdapat pada kedua ujungnya. Contohnya garis dengan titik ujung A dan B, maka garis tersebut dinamakan garis AB.
Bidang adalah perluasan dari garis-garis yang terhubung menjadi satu permukaan datar dan mempunyai ukuran panjang dan lebar. Penamaan bidang dapat mengambil dari huruf-huruf yang terletak pada sudutnya. Contoh sebuah bidang dengan sudut-sudut A, B, C, D. Maka bidang tersebut dinamakan bidang ABCD.
Kedudukan Titik, Garis, Dan Bidang
Titik, garis, dan bidang memiliki hubungan dalam suatu kedudukan. Berikut adalah penjelasan mengenai kedudukan antara titik, garis, dan bidang, lengkap beserta gambarnya.
1. Kedudukan Titik Terhadap Garis

Secara umum, kedudukan titik terhadap garis dibagi menjadi dua. Yakni titik terletak pada garis dan titik terletak di luar garis.
a. Titik Terletak Pada Garis
Jika suatu titik dilalui garis, maka titik terletak pada garis tersebut. Atau dapat diartikan bahwa garis melalui titik. (Gambar 1.a)
b. Titik Terletak Di Luar Garis
Jika suatu titik tidak dilalui garis, maka titik terletak di luar garis tersebut. Atau dapat diartikan bahwa garis tidak melalui titik. (Gambar 1.b)
2. Kedudukan Titik Terhadap Bidang

Sama halnya dengan kedudukan titik terhadap garis, kedudukan titik terhadap bidang juga dibagi menjadi dua, yaitu titik terletak pada bidang dan titik terletak di luar bidang.
a. Titik Terletak Pada Bidang
Jika suatu titik dilewati bidang, maka titik terletak pada bidang tersebut. Atau dapat diartikan bahwa bidang melewati titik. (Gambar 2.a)
b. Titik Terletak Di Luar Bidang
Jika suatu titik tidak dilewati bidang, maka titik terletak di luar bidang tersebut. Atau dapat diartikan bahwa tidak tidak melewati titik. (Gambar 2.b)
3. Kedudukan Garis Terhadap Garis

Dua buah garis kemungkinan dapat memiliki kedudukan antara yang satu dengan lainnya. Kedudukan garis terhadap garis dapat saling berhimpit, saling berpotongan, saling sejajar, dan saling bersilangan.
a. Dua Garis Saling Berhimpit
Dua garis dikatakan saling berhimpit jika terdapat lebih dari satu titik persekutuan. (Gambar 3.a)
b. Dua Garis Saling Berpotongan
Dua garis dikatakan saling berpotongan jika terdapat tepat satu titik persekutuan. (Gambar 3.b)
c. Dua Garis Saling Sejajar
Dua garis dikatakan saling sejajar jika tidak ada satupun titik persekutuan. (Gambar 3.c)
d. Dua Garis Saling Bersilangan
Dua garis dikatakan saling berpotongan jika tidak saling berpotongan, tidak saling sejajar dan tidak terletak pada satu bidang. (Gambar 3.d)
4. Kedudukan Garis Terhadap Bidang

Kemungkinan kedudukan garis terhadap bidang adalah garis terletak pada bidang, sejajar, dan berpotongan.
a. Garis Terletak Pada Bidang
Sebuah garis dikatakan terletak pada bidang, jika terdapat lebih dari satu titik persekutuan antara garis dengan bidang. (Gambar 4.a)
b. Garis Sejajar Pada Bidang
Sebuah garis dikatakan sejajar bidang, jika tidak terdapat titik persekutuan sama sekali antara garis dengan bidang. (Gambar 4.b)
c. Garis Berpotongan Pada Bidang
Sebuah garis dikatakan berpotongan bidang, jika terdapat tepat satu titik persekutuan (titik tembus) antara garis dengan bidang. (Gambar 4.c)
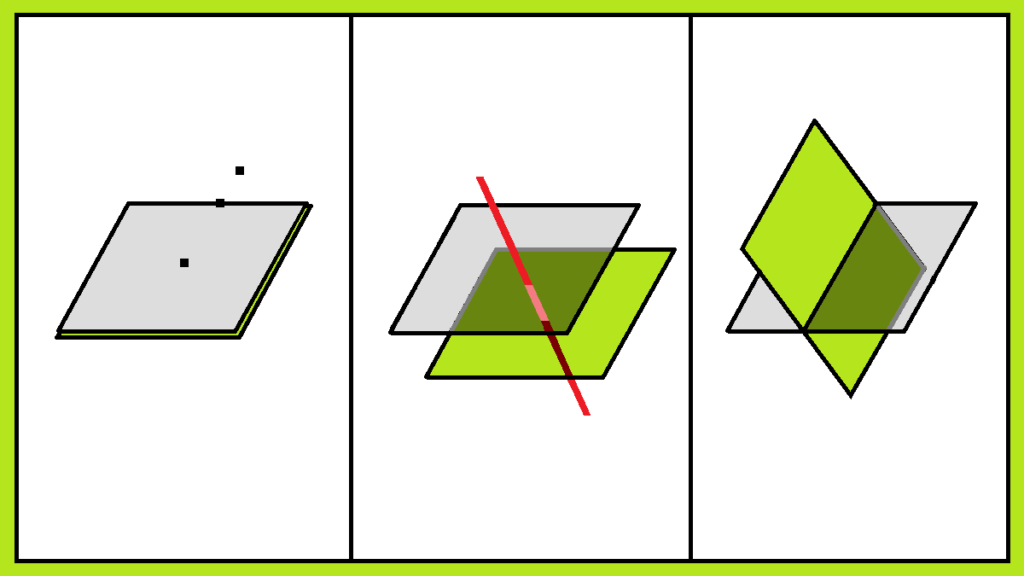
5. Kedudukan Bidang Terhadap Bidang
Kemungkinan kedudukan bidang terhadap bidang adalah saling berhimpit, sejajar, dan berpotongan.
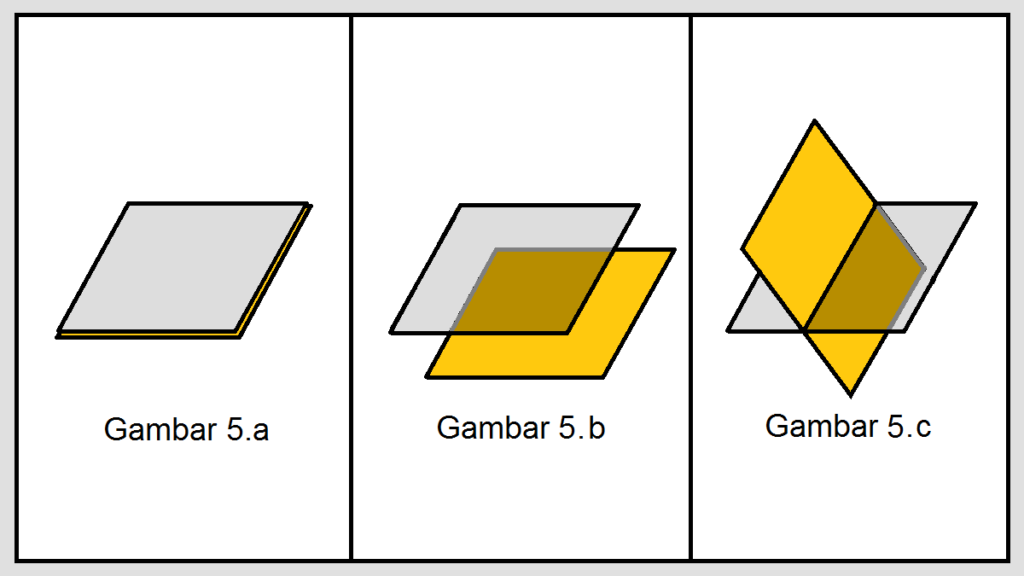
a. Dua Bidang Saling Berimpit
Dua buah bidang dikatakan saling berhimpit jika setiap titik di satu bidang terletak pada bidang lainya. (Gambar 5.a)
b. Dua Bidang Saling Sejajar
Dua buah bidang dikatakan saling sejajar jika tidak terdapat satu pun titik persekutuan. (Gambar 4.b)
c. Dua Bidang Saling Berpotongan
Dua buah bidang dikatakan saling berpotongan jika terdapat tepat satu garis persekutuan. (Gambar 4.c)
Contoh Soal

Perhatikan gambar di atas! Tentukanlah kedudukan antara titik, garis, dan bidang berikut ini.
1. Titik yang terletak pada garis AB
2. Titik yang terletak di luar garis AB
3. Titik yang terletak pada bidang ABCD
4. Titik yang terletak di luar bidang ABCD
5. Garis yang berhimpit dengan garis AB
6. Garis yang berpotongan dengan garis AB
7. Garis yang sejajar dengan garis AB
8. Garis yang bersilangan dengan garis AB
9. Garis yang terletak pada bidang ABCD
10. Garis yang sejajar bidang dengan ABCD
11. Garis yang berpotongan dengan bidang ABCD
12. Bidang yang berhimpit dengan bidang ABCD
13. Bidang yang sejajar dengan bidang ABCD
14. Bidang yang berpotongan dengan bidang ABCD
Pembahasan:
1. Titik yang terletak pada garis AB adalah titik A dan B.
2. Titik yang terletak di luar garis AB adalah titik C, D, E, F, G, H.
3. Titik yang terletak pada bidang ABCD adalah titik A, B, C, D.
4. Titik yang terletak di luar bidang ABCD adalah titik E, F, G, H.
5. Garis yang berhimpit dengan garis AB adalah garis AB.
6. Garis yang berpotongan dengan garis AB adalah garis BC, BF, AD, AE.
7. Garis yang sejajar dengan garis AB adalah garis DC, EF, HG.
8. Garis yang bersilangan dengan garis AB adalah garis CG, DH, FG, EH.
9. Garis yang terletak pada bidang ABCD adalah garis AB, BC, CD, DA.
10. Garis yang sejajar bidang dengan ABCD adalah garis EF, FG, GH, HE.
11. Garis yang berpotongan dengan bidang ABCD adalah garis AE, BF, CG, DH.
12. Bidang yang berhimpit dengan bidang ABCD adalah bidang ABCD.
13. Bidang yang sejajar dengan bidang ABCD adalah bidang EFGH.
14. Bidang yang berpotongan dengan bidang ABCD adalah bidang ABFE, BCGF, DCGH, ADHE.
Demikianlah pembahasan mengenai kedudukan titik, garis, dan bidang. Semoga bermanfaat.
Baca Juga :