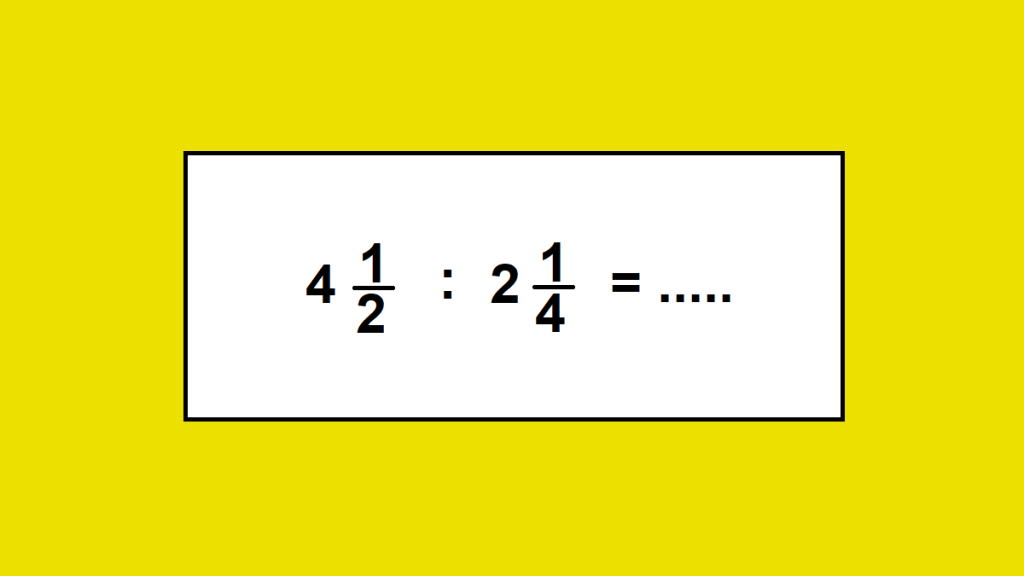
Cara Menghitung Pembagian Pecahan Campuran – Cara menghitung pecahan campuran berbeda dengan pecahan biasa. Setelah sebelumnya telah dipelajari perkalian pecahan campuran, pada kesempatan kali ini akan dibahas tentang cara menghitung pembagian pecahan campuran beserta contoh soalnya.
Pecahan campuran adalah bilangan pecahan yang terdiri dari bilangan bulat dan pecahan, serta ditulis dalam bentuk a b/c. Contoh pecahan campuran seperti 3 2/5, dimana 3 merupakan bilangan bulat dan 2/5 sebagai bentuk pecahan.
Rumus menghitung pecahan campuran adalah mengubah pecahan campuran menjadi pecahan biasa. Setelah diubah, kemudian menghitungnya dengan konsep operasi hitung pecahan. Nah, berikut akan dijelaskan bagaimana cara menghitung pembagian pecahan campuran.
Cara Menghitung Pembagian Pecahan Campuran
Untuk menghitung pembagian pecahan campuran, langkah pertama adalah mengubah pecahan campuran menjadi pecahan biasa.
Untuk mengubah pecahan campuran menjadi pecahan biasa, langkah-langkahnya adalah sebagai berikut:
- Kalikan penyebut dengan bilangan bulat
- Jumlahkah hasilnya dengan pembilang
- Hasil akhir dijadikan pembilang, untuk penyebutnya tetap
Setelah diubah menjadi pecahan biasa, lakukan konsep pembagian pecahan dengan rumus:
- Membalikan posisi pembilang jadi penyebut pada pecahan pembagi
- Mengubah operasi pembagian menjadi perkalian
- Kalikan pembilang dengan pembilang, penyebut dengan penyebut
Agar lebih mudah memahami langkah-langkah pembagian pecahan campuran, silahkan simak contoh soal berikut ini.
Contoh Soal
Berikut adalah contoh soal menghitung pembagian pecahan campuran beserta langkah-langkah penyelesaiannya.
1. 4 1/2 : 2 1/4 = …..
Penyelesaian:
Langkah pertama: mengubah pecahan campuran menjadi pecahan biasa
4 1/2 = (2 x 4 + 1)/2 = 9/2
2 1/4 = (4 x 2 + 1)/4 = 9/4
Langkah kedua: menghitung pembagian pecahan
9/2 : 9/4 = 9/2 x 4/9 = (9 x 4)/(2 x 9) = 36/18
36/18 = 2
Jadi, hasil pembagian dari 4 1/2 : 2 1/4 = 2.
2. 6 2/3 : 3 5/6 = …..
Penyelesaian:
Langkah pertama: mengubah pecahan campuran menjadi pecahan biasa
6 2/3 = (3 x 6 + 2)/3 = 20/3
3 5/6 = (6 x 3 + 5)/6 = 23/6
Langkah kedua: menghitung pembagian pecahan
20/3 : 23/6 = 20/3 x 6/23 = (20 x 6)/(3 x 23) = 120/69
120/69 = 1 51/69 = 1 17/23
Jadi, hasil pembagian dari 6 2/3 : 3 5/6 = 1 17/23.
3. 10 3/5 : 5 1/3 = …..
Penyelesaian:
Langkah pertama: mengubah pecahan campuran menjadi pecahan biasa
10 3/5 = (5 x 10 + 3)/5 = 53/5
5 1/3 = (3 x 5 + 1)/3 = 16/3
Langkah kedua: menghitung pembagian pecahan
53/5 : 16/3 = 53/5 x 3/16 = (53 x 3)/(5 x 16) = 159/80
159/80 = 1 79/80
Jadi, hasil pembagian dari 10 3/5 : 5 1/3 = 1 79/80.
4. 3 1/2 : 1 1/4 = …..
Penyelesaian:
Langkah pertama: mengubah pecahan campuran menjadi pecahan biasa
3 1/2 = (2 x 3 + 1)/2 = 7/2
1 1/4 = (4 x 1 + 1)/4 = 5/4
Langkah kedua: menghitung pembagian pecahan
7/2 : 5/4 = 7/2 x 4/5 = (7 x 4)/(2 x 5) = 28/10
28/10 = 2 8/10 = 2 4/5
Jadi, hasil pembagian dari 3 1/2 : 1 1/4 = 2 4/5.
5. 5 1/3 : 1 2/3 = …..
Penyelesaian:
Langkah pertama: mengubah pecahan campuran menjadi pecahan biasa
5 1/3 = (3 x 5 + 1)/3 = 16/3
1 2/3 = (3 x 1 + 2)/3 = 5/3
Langkah kedua: menghitung pembagian pecahan
16/3 : 5/3 = 16/3 x 3/5 = (16 x 3)/(3 x 5) = 48/15
48/15 = 3 3/15 = 3 1/5
Jadi, hasil pembagian dari 5 1/3 : 1 2/3 = 3 1/5.
Demikianlah pembahasan mengenai cara menghitung pembagian pecahan campuran dan contoh soalnya. Semoga bermanfaat.
Baca Juga :







