Contoh Soal Bangun Datar Gabungan – Bangun datar gabungan merupakan sebuah bangun yang dibentuk oleh beberapa bangun datar.
Bangun datar gabungan bisa dibentuk oleh persegi dan persegi panjang, segitiga dan trapesium, jajar genjang dan belah ketupat, atau layang-layang dan lingkaran.
Meskipun terlihat seperti bentuk tidak beraturam, namun bangun datar gabungan tetap dapat dihitung luas dan kelilingnya.
Untuk menghitung bangun datar gabungan, diperlukan rumus-rumus luas dan keliling bangun datar.
| Bangun Datar | Luas | Keliling |
| Persegi | s x s | 4 x s |
| Persegi panjang | p x l | 2 x (p + l) |
| Segitiga | 1/2 x a x t | s + s + s |
| Trapesium | 1/2 x (a + b) x t | s + s + s + s |
| Jajar genjang | a x t | 2 x (a + b) |
| Belah ketupat | 1/2 x d1 x d2 | 4 x s |
| Layang-layang | 1/2 x d1 x d2 | s + s + s + s |
| Lingkaran | π x r² | 2 x π x r |
Contoh Soal Bangun Datar Gabungan
Berikut merupakan pemabahasan contoh soal bagaimana cara menghitung luas dan keliling bangun datar gabungan.
Contoh Soal 1
Hitunglah luas dan keliling bangun gabungan pada gambar di bawah ini!
Penyelesaian:
Bangun tersebut terdiri dari segitiga dan trapesium
1. Menghitung Luas Bangun Gabungan
a. Luas Segitiga
Karena ukuran alas segitiga belum diketahui, maka cari terlebih dahulu.
a = 2 (√5² – 4²)
a = 2 (√25 – 16)
a = 2 √9
a = 2 x 3 = 6 cm
L = 1/2 x a x t
L = 1/2 x 6 x 4
L = 12 cm²
b. Luas Trapesium
Ukuran sisi sejajar trapesium yang belum diketahui dapat ditentukan dengan cara:
s = 6 + alas segitiga + 6
s = 6 + 6 + 6
s = 18 cm
L = 1/2 x (a + b) x t
L = 1/2 x (15 + 18) x 7
L = 115,5 cm²
c. Luas Bangun Gabungan
L = luas segitiga + luas trapesium
L = 12 + 115,5
L = 127,5 cm²
Jadi, luas bangun gabungan tersebut adalah 127,5 cm².
2. Menghitung Keliling Bangun Gabungan
Keliling bangun gabungan dapat dihitung dengan cara menjumlahkan seluruh sisi luarnya saja.
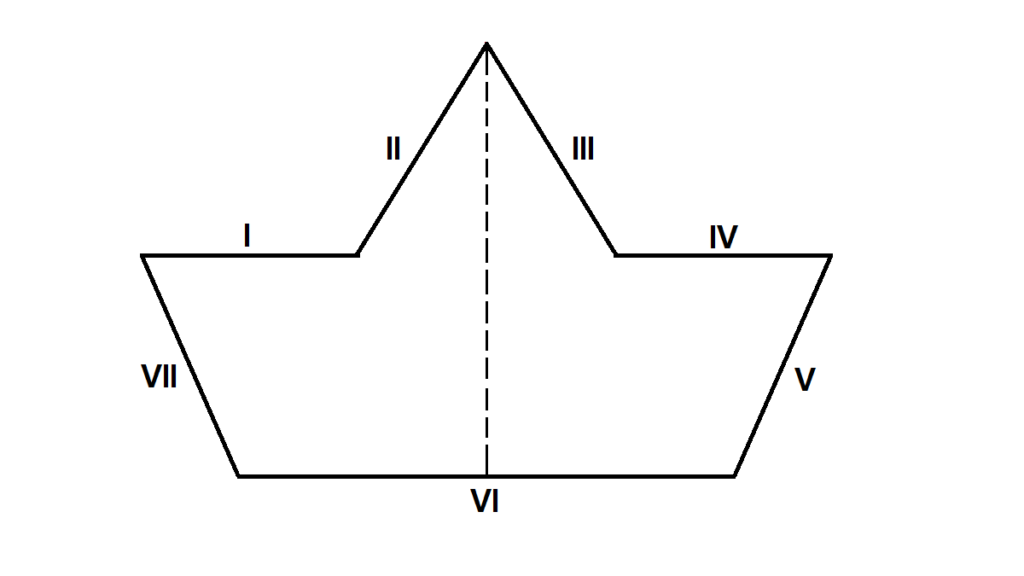
K = I + II + III + IV + V + VI + VII
K = 6 + 5 + 5 + 6 + 8 + 15 + 8
K = 53 cm
Jadi, keliling bangun gabungan tersebut adalah 53 cm.
Contoh Soal 2
Tentukan luas dan keliling bangun gabungan di bawah ini!
Penyelesaian:
Bangun tersebut terdiri dari persegi dan persegi panjang
1. Menghitung Luas Bangun Gabungan
a. Luas Persegi
L = s x s
L = 10 x 10
L = 100 cm²
b. Luas Persegi Panjang
L = p x l
L = 25 x 12
L = 300 cm²
c. Luas bangun gabungan
L = luas persegi + luas persegi panjang
L = 100 + 300
L = 400 cm²
Jadi, luas bangun gabungan tersebut adalah 400 cm².
2. Menghitung Keliling Bangun Gabungan
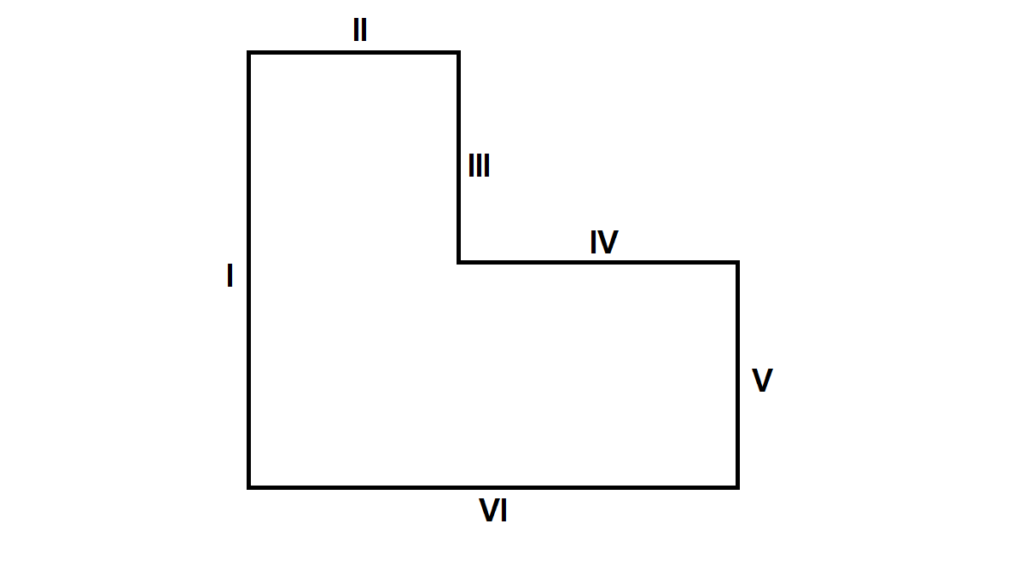
K = I + II + III + IV + V + VI
K = (12 + 10) + 10 + 10 + (25 – 10) + 12 + 25
K = 22 + 10 + 10 + 15 + 12 + 25
K = 94 cm
Jadi, keliling bangun gabungan tersebut adalah 94 cm.
Contoh Soal 3
Hitunglah luas dan keling bangun gabungan di bawah ini!
Penyelesaian:
Bangun tersebut terdiri dari persegi panjang dan dua buah setengah lingkaran
1. Menghitung Luas Bangun Gabungan
a. Luas Persegi Panjang
L = p x l
L = 10 x 7
L = 70 cm²
b. Luas Setengah Lingkaran
Jari-jari 1/2 lingkaran = 1/2 lebar persegi panjang
r = 1/2 x 7
r = 3,5 cm
L = 1/2 x π x r²
L = 1/2 x 22/7 x 3,5 x 3,5
L = 19,25 cm²
c. Luas Bangun Gabungan
L = luas persegi panjang + luas 1/2 lingkaran + luas 1/2 lingkaran
L = 70 + 19,25 + 19,25
L = 108,5 cm²
Jadi, luas bangun gabungan tersebut adalah 108,5 cm².
2. Menghitung Keliling Bangun Gabungan
Mencari keliling setengah lingkaran terlebih dahulu:
K = 1/2 x 2 x π x r
K = 1/2 x 2 x 22/7 x 3,5
K = 11 cm
Kemudian menghitung kelilingnya:
K = I + II + III + IV
K = 10 + 11 + 10 + 11
K = 42 cm
Jadi, keliling bangun gabungan tersebut adalah 42 cm.
Contoh Soal 4
Tentukan luas bangun datar gabungan pada gambar di bawah ini!
Penyelesaian:
Bangun tersebut terdiri dari segitiga, persegi, dan setengah lingkaran
1. Menghitung Luas Bangun Gabungan
a. Luas Segitiga
Karena ukuran alas segitiga belum diketahui, maka cari terelbih dahulu:
a = 2 (√10² – 8²)
a = 2 (√100 – 64)
a = 2 √36
a = 2 x 6 = 12 cm
L = 1/2 x a x t
L = 1/2 x 12 x 8
L = 48 cm²
b. Luas Persegi
L = s x s
L = 12 x 12
L = 144 cm²
c. Luas 1/2 Lingkaran
Jari-jari lingkaran = 1/2 sisi persegi
r = 1/2 x 12
r = 6 cm
L = 1/2 x π x r²
L = 1/2 x 3,14 x 6 x 6
L = 56,52 cm²
d. Luas Bangun Gabungan
L = luas segitiga + luas persegi + luas 1/2 lingkaran
L = 48 + 144 + 56,52
L = 248,52 cm²
Jadi, luas bangun gabungan tersebut adalah 248,52 cm².
2. Menghitung Keliling Bangun Gabungan
Mencari keliling setengah lingkaran terlebih dahulu:
K = 1/2 x 2 x π x r
K = 1/2 x 2 x 3,14 x 6
K = 18,84 cm
Kemudian menghitung kelilingnya:
K = I + II + III + IV + V
K = 12 + 18,84 + 12 + 10 + 10
K = 62,84 cm
Jadi, keliling bangun gabungan tersebut adalah 62,84 cm.
Demikianlah pembahasan mengenai contoh soal menghitung bangun datar gabungan. Semoga bermanfaat.
Baca Juga :
