Cara Menentukan Banyaknya Anggota Himpunan Bagian – Dalam matematika, himpunan memiliki beberapa jenis operasi perhitungan. Salah satunya adalah himpunan bagian. Nah, pada artikel ini akan dibahas tentang bagaimana cara menentukan banyaknya anggota pada himpunan bagian.
Pengertian Himpunan Bagian
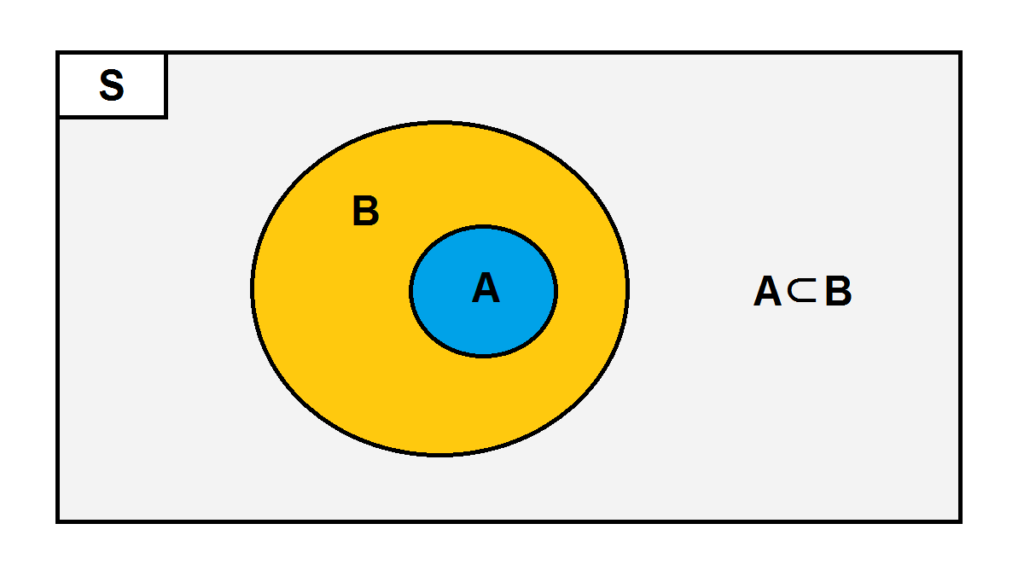
Himpunan bagian atau subset adalah suatu himpunan yang tersusun dari anggota himpunan lainnya yang cakupannya lebih luas. Lambang himpunan bagian dinyatakan dengan notasi ⊂.
Jika himpunan A merupakan himpunan bagian B, maka setiap anggota himpunan A adalah anggota himpunan B. Himpunan A bagian dari himpunan B dapat dituliskan dengan A ⊂ B atau B ⊃ A.
Contoh:
A = {1, 2, 3}
B = {1, 2, 3, 4, 5}
Maka, A ⊂ B
Jika terdapat anggota himpunan A bukan anggota B, maka artinya A bukan himpunan bagian dari himpunan B. Notasi untuk meyatakan himpunan A bukan bagian dari himpunan B dituliskan dengan A ⊄ B.
Contoh:
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
Maka, A ⊄ B
Cara Menentukan Banyaknya Anggota Himpunan Bagian
Untuk menentukan banyaknya anggota himpunan bagian dapat menggunakan rumus:
| 2n |
n adalah jumlah anggota dari himpunan.
Contoh:
Himpunan A = {a, b, c, d, e}. Tentukan banyaknya anggota himpunan bagian dari A!
Penyelesaian:
Himpunan A terdiri dari 5 anggota
Banyaknya anggota himpunan bagian dari himpunan A adalah:
2n = 25 = 2 x 2 x 2 x 2 x 2 = 32.
Kemungkinan anggota himpunan bagian dari himpunan A = {a, b, c, d, e} adalah:
- Anggota himpunan bagian A berupa himpunan kosong sebanyak 1, yaitu himpunan kosong { }
- Anggota himpunan A dengan 1 anggota ada sebanyak 5, yaitu: {{a}, {b}, {c}, {d}, {e}}
- Anggota himpunan bagian A dengan 2 anggota ada 10, yaitu: {{a, b}, {a, c}, {a, d}, {a, e}, {b, c}, {b, d}, {b, e}, {c, d}, {c, e}, {d, e}}
- Anggota himpunan bagian A dengan 3 anggota ada 10, yaitu: {{a, b, c}, {a, b, d}, {a, b, e}, {a, c, d}, {c, c, e}, {a, d, e}, {b, c, d}, {b, c, e}, {b, d, e}, {c, d, e}}
- Anggota himpunan bagian A dengan 4 anggota ada 5, yaitu: {{a, b, c, d}, {a, b, c, e}, {b, c, d, e}, {a, c, d, e}, {a, b, d, e}}
- Anggota himpunan bagian A dengan 5 anggota ada 1, yaitu: {(a, b, c, d, e)}
Demikianlah pembahasan mengenai cara menentukan banyaknya anggota himpunan bagian beserta contohnya. Semoga bermanfaat.
Baca Juga :