Rumus Luas Permukaan Prisma – Prisma merupakan bangun ruang tiga dimensi yang memiliki volume dan luas permukaan. Nah, pada kesempatan kali ini akan dibahas tentang rumus luas permukaan prisma dan contoh soalnya.
Prisma adalah bangun ruang yang dibatasi oleh sisi alas dan sisi atas berbentuk segi-n kongruen, serta sisi tegak berbentuk segi empat. Prisma memiliki beberapa jenis, diantaranya yaitu prisma segitiga, prisma segi empat, prisma segi lima, dan seterusnya.
Setiap jenis prisma memiliki pola jaring-jaring yang berbeda. Begitu juga dengan rumus yang digunakan untuk menghitung luas permukaan dari berbagai jenis prisma.
Sebelum mempelajari rumus luas permukaan prisma, berikut akan dijelaskan beberapa jenis prisma. Berdasarkan bentuk alasnya, prisma dibedakan menjadi beberapa jenis, diantaranya yaitu:
- Prisma Segitiga, adalah prisma yang mempunyai sisi alas dan sisi atas berbentuk segitiga
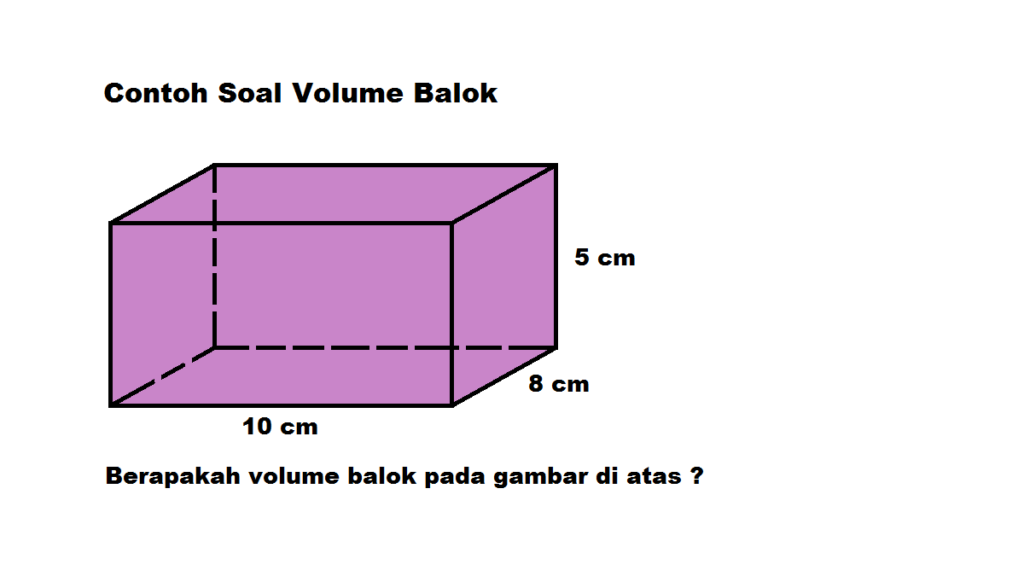
- Prisma Segi Empat, prisma yang mempunyai sisi alas dan sisi atas berbentuk segi empat. Contoh prisma segi empat yaitu kubus dan balok
- Prisma Segi Lima, adalah prisma yang mempunyai sisi alas dan sisi atas berbentuk segi lima
- Prisma Segi Enam, adalah prisma yang mempunyai sisi alas dan sisi atas berbentuk segi enam
- Prisma Segi Tak Terhingga, adalah prisma yang mempunyai sisi alas dan atas berbentuk segi-n tak terhingga. Prisma ini sering disebut tabung
Rumus Luas Permukaan Prisma Dan Contoh Soal
Jika kita membuka bangun prisma, maka akan diperoleh jaring-jaring prisma yang terdiri dari dua bidang sisi yang sama dan sisi tegak prisma yang berbentuk persegi panjang. Secara umum, rumus untuk menghitung luas permukaan prisma adalah:
| L = (2 x LA) + (KA x T) |
Keterangan:
L = luas permukaan prisma
LA = luas alas prisma
KA = keliling alas prisma
T = tinggi prisma
Kita juga dapat mengembangkan rumus tersebut untuk menghitung luas permukaan dari berbagai jenis prisma. Berikut penjelasannya.
A. Luas Permukaan Prisma Segitiga
Untuk menghitung luas permukaan prisma segitiga, kita harus mengetahui rumus luas dan keliling segitiga.
| Luas Segitiga = 1/2 x alas x tinggi |
| Keliling Segitiga = s + s + s |
Dari rumus tersebut, maka diperoleh rumus untuk menghitung luas permukaan prisma segitiga adalah sebagai berikut:
| L = [2 x (1/2 x a x t)] + [(s + s + s ) x T] |
Keterangan:
L = luas permukaan prisma segitiga
a = alas segitiga
t = tinggi segitiga
s = sisi segitiga
T = tinggi prisma
Contoh Soal
Sebuah prisma segitiga siku-siku mempunyai ukuran sisi alasnya 3 cm, 4 cm, dan 5 cm. JIka tinggi prisma 10 cm, berapakah luas permukaan prisma segitiga siku-siku tersebut?
Penyelesaian:
L = [2 x (1/2 x a x t)] + [(s + s + s ) x T]
L = [2 x (1/2 x 3 x 4)] + [(3 + 4 + 5 ) x 10]
L = [2 x 6] + [12 x 10]
L = 12 + 120
L = 132 cm²
Jadi, luas permukaan prisma segitiga siku-siku tersebut adalah 132 cm².
B. Luas Permukaan Prisma Segi Empat
Untuk menghitung luas permukaan prisma segi empat, kita harus mengetahui rumus-rumus luas dan keliling bangun segi empat, seperti persegi, persegi panjang, belah ketupat, dan trapesium.
| Bangun | Luas | Keliling |
| Persegi | s x s | 4 x s |
| Persegi Panjang | p x l | 2 x (p + l) |
| Belah Ketupat | 1/2 x d1 x d2 | 4 x s |
| Jajar Genjang | a x t | s + s + s + s |
| Layang-layang | 1/2 x d1 x d2 | s + s + s + s |
| Trapesium | 1/2 x (jumlah sisi sejajar) x t | s + s + s + s |
1. Luas Permukaan Prisma Persegi
Rumus untuk menghitung luas permukaan luas permukaan prisma dengan sisi alas berbentuk persegi adalah sebagai berikut:
| L = [2 x (s x s)] + [(4 x s) x t] |
Keterangan:
L = luas permukaan
s = sisi alas
t = tinggi prisma
Contoh Soal
Sebuah prisma segi empat mempunyai sisi alas berbentuk persegi dengan ukuran sisi 10 cm. Jika tinggi prisma sama dengan panjang sisi alasnya, berapakah luas permukaan prisma tersebut?
Penyelesaian:
L = [2 x (s x s)] + [(4 x s) x t]
L = [2 x (10 x 10)] + [(4 x 10) x 10]
L = [2 x 100] + [40 x 10]
L = 200 + 400
L = 600 cm²
Jadi, luas permukaan prisma tersebut adalah 600 cm².
2. Luas Permukaan Prisma Persegi Panjang
Rumus untuk menghitung luas permukaan luas permukaan prisma dengan sisi alas berbentuk persegi panjang adalah sebagai berikut:
| L = [2 x (p x l)] + [[2 x (p + l)] x t] |
Keterangan:
L = luas permukaan
p = panjang alas
l = lebar alas
t = tinggi prisma
Contoh Soal
Sebuah prisma segi empat memiliki sisi alas berbentuk persegi panjang dengan ukuran 8 cm dan 5 cm. Jika tinggi prisma 10 cm, berapakah luas permukaan prisma?
Penyelesaian:
L = [2 x (p x l)] + [[2 x (p + l)] x t]
L = [2 x (8 x 5)] + [[2 x (8 + 5)] x 10]
L = [2 x 40] + [26 x 10]
L = 80 + 260
L = 340 cm²
Jadi, luas permukaan prisma adalah 340 cm².
3. Luas Permukaan Prisma Belah Ketupat
Rumus untuk menghitung luas permukaan luas permukaan prisma dengan sisi alas berbentuk belah ketupat adalah sebagai berikut:
| L = [2 x (1/2 x d1 x d2)] + [(4 x s) x t] |
Keterangan:
L = luas permukaan
d1,d2 = diagonal alas
s = sisi alas
t = tinggi prisma
Contoh Soal
Sebuah prisma segi empat memiliki sisi alas berbentuk belah ketupat dengan ukuran sisi 5 cm, sedangkan panjang diagonalanya 6 cm dan 8 cm. jika tinggi prisma 10 cm. Hitunglah berapa luas permukaan prisma tersebut!
Penyelesaian:
L = [2 x (1/2 x d1 x d2)] + [(4 x s) x t]
L = [2 x (1/2 x 6 x 8)] + [(4 x 5) x 10]
L = [2 x 7] + [20 x 10]
L = 14 + 200
L = 214 cm²
Jadi, luas permukaan tersebut adalah 214 cm².
4. Luas Permukaan Prisma Segi Tak Terhingga
Untuk menghitung luas permukaan prisma dengan sisi alas segi-n tak terhingga, kita harus mengetahui rumus luas dan keliling lingkaran.
| Luas Lingkaran = π × r² |
| Keliling Lingkaran = 2 × π × r |
Keterangan:
π = 22/7 atau 3,14
r = jari-jari lingkaran
Nah, untuk menghitung luas permukaan prisma segi-n tak terhingga atau tabung adalah sebagai berikut:
| L = [2 x (π x r²)] + [(2 x π x r) x t] |
Keterangan:
L = luas permukaan
π = 22/7 atau 3,14
r = jari-jari alas
t = tinggi prisma
Contoh Soal
Sebuah prisma memiliki sisi alas berbentuk lingkaran dengan jari-jari 7 cm dan tinggi 10 cm. Berapakah luas permukaan prisma tersebut?
Penyelesaian:
L = [2 x (π x r²)] + [(2 x π x r) x t]
L = [2 x (22/7 x 7²)] + [(2 x 22/7 x 7) x 10]
L = [2 x (22/7 x 49)] + [(2 x 22/7 x 7) x 10]
L = [2 x 154] + [44 x 10]
L = 308 + 440
L = 748 cm²
Jadi, luas permukaan prisma tersebut adalah 748 cm².
Demikianlah pembahasan mengenai rumus luas permukaan prisma dan contoh soalnya. Semoga bermanfaat.
Baca Juga :
- Rumus Luas Permukaan Limas Segitiga Dan Segi Empat
- Rumus Luas Permukaan Kerucut Beserta Contoh Soalnya
- Rumus Volume Prisma Segitiga
- Rumus Luas Permukaan Bola Beserta Contoh Soalnya
- Rumus Menghitung Volume Kubus Dan Balok