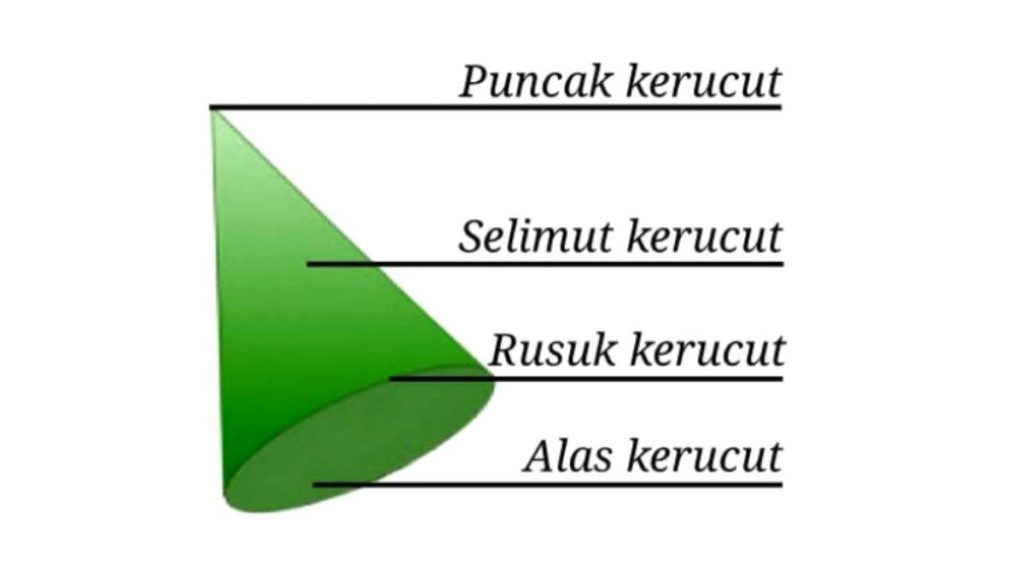
Bagian-Bagian Kerucut Dan Rumusnya – Kerucut adalah suatu bangun ruang tiga dimensi yang memiliki volume atau isi. Setiap bangun ruang memiliki bagian-bagian penyusunnya. Lalu tahukah apa saja bagian-bagian yang ada pada bangun ruang kerucut? Simak penjelasan berikut ini mengenai bagian-bagian kerucut dan rumusnya.
Pengertian Kerucut
Kerucut adalah bangun ruang sisi lengkung seperti halnya tabung dan bola. Bangun ini menyerupai bentuk limas dengan sisi alasnya berbentuk lingkaran. Kerucut memiliki 2 buah sisi, 1 buah rusuk, dan 1 buah titik sudut.
Kerucut memiliki dua sisi yang terdiri dari sisi alas berbentuk lingkaran dan sisi tegak/selimut yang berbentuk juring lingkaran. Sisi selimut kerucut menguncup pada ujungnya dan membentuk sebuah titik sudut.
Kerucut dapat dibentuk dari sebuah segitiga siku-siku yang diputar sejauh 360 derajat, dimana sisi siku-sikunya sebagai pusat putaran. Untuk lebih jelasnya, silahkan perhatikan gambar di bawah ini.

Kerucut pada gambar di atas dibentuk dari segitiga siku-siku AOT yang diputar satu putaran penuh (360 derajat) dengan sisi OT sebagai pusat putarannya.
Ciri-Ciri Kerucut
Dari penjelasan di atas, maka dapat disimpulkan bahwa bangun kerucut memiliki 1 titik sudut yang terletak di ujung selimut serta 1 rusuk berbentuk lingkaran yang menghubungkan sisi alas dan sisi selimut. Ada pun ciri-ciri kerucut yaitu sebagai berikut:
- Kerucut memiliki 2 buah bidang sisi (1 sisi alas berbentuk lingkaran dan 1 sisi selimut berbentuk juring lingkaran)
- Kerucut memiliki 1 buah rusuk berbentuk lingkaran yang menghubungkan sisi alas dan sisi selimutnya.
- Kerucut memiliki 1 titik puncak yang berada pada ujung sisi selimutnya.
- Kerucut merupakan bangun ruang limas yang alasnya berbentuk lingkaran.
- Kerucut memiliki jaring-jaring kerucut yaitu lingkaran dan juring lingkaran.
Bagian-Bagian Kerucut Dan Rumusnya
Untuk memahami apa saja bagian-bagian pada bangun kerucut, perhatikan gambar kerucut di bawah ini.
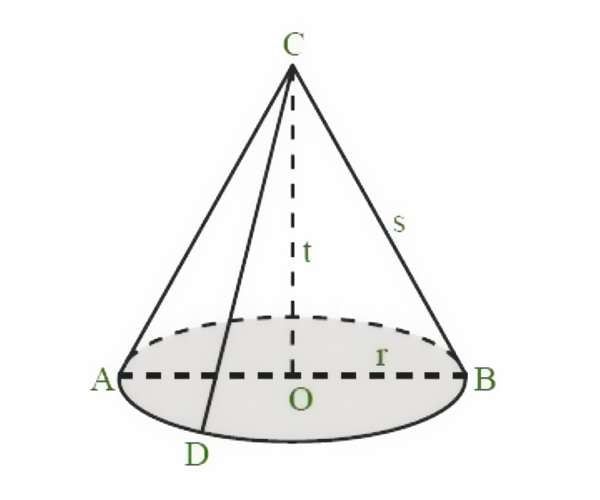
Berdasarkan gambar di atas, maka diperoleh kesimpulan bahwa bangun kerucut tersebut memiliki bagian-bagian sebagai berikut:
a. Sisi Alas Kerucut
Sisi alas kerucut adalah sisi yang berbentuk lingkaran yang diarsir pada gambar di atas. Untuk menghitung luas alas kerucut yaitu dengan menggunakan rumus luas lingkaran.
| Rumus Luas Alas Kerucut = π × r² |
b. Jari-Jari Kerucut (r)
Jari-jari kerucut adalah jarak antara titik pusat lingkaran alas dengan rusuk kerucut. Pada gambar di atas, jari-jari kerucut yaitu ruas garis OA dan ruas garis OB yang ukurannya setengah dari panjang AB. Panjang jari-jari kerucut adalah setengah diameter lingkaran kerucut.
| r = 1/2 × diameter |
c. Diameter Alas Kerucut (d)
Diameter alas kerucut adalah jarak antar lengkungan rusuk kerucut yang melewati titip pusat lingkaran alas kerucut. yaitu ruas garis AB yang panjangnya adalah 2 × jari-jari sisi alas kerucut.
| d = 2 × r |
d. Tinggi Kerucut (t)
Tinggi kerucut adalah jarak dari titik puncak kerucut ke pusat bidang alas. Pada gambar di atas, tinggi kerucut ditunjukan oleh ruas garis CO.
e. Selimut Kerucut
Selimut kerucut adalah sisi tegak kerucut yang apabila dibongkar merupakan jaring-jaring kerucut yang berbentuk jurung lingkaran. Rumus untuk menghitung selimut kerucut adalah:
| Rumus Luas Selimut Kerucut = π × r × s |
f. Garis Pelukis Kerucut (s)
Garis pelukis adalah garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke lengkungan rusuk kerucut. Hubungan antara r, s, dan t pada kerucut tersebut di atas dapat dinyatakan dengan persamaan-persamaan rumus teorema pythagoras segitiga siku-siku, yaitu sebagai berikut:
| s² = r² + t² |
| r² = s² − t² |
| t² = s² − r² |
g. Jaring-Jaring Kerucut
Kerucut mempunyai jaring-jaring yang terdiri dari satu lingkaran dan juring lingkaran yang. Di bawah ini merupakan salah satu contoh jaring-jaring pada kerucut.

h. Volume Dan Luas Permukaan Kerucut
Volume kerucut adalah seberapa besar ruang di dalam kerucut yang mampu ditempati. Sedangkan luas permukaan kerucut merupakan julah seluruh luas sisinya. Untuk menghitung volume kerucut dan luas permukaan kerucut dapat menggunakan rumus sebagai berikut:
Rumus Volume Kerucut
| V = 1/3 × Luas Alas × Tinggi |
| V = 1/3 × πr² × t |
Rumus Luas Permukaan Kerucut
| L = Luas Alas + Luas Selimut |
| L = π × r² + π × r × s |
| L = πr × (r + s) |
Contoh Soal Menghitung Volume Dan Luas Permukaan Kerucut
1. Sebuah kerucut memiliki jari-jari alas 7 cm dan tinggi 15 cm. Hitunglah berapa volume kerucut tersebut!
Penyelesaian:
V = 1/3 × πr² × t
V = 1/3 × 22/7 x 7² × 15
V = 1/3 × 2310
V = 770 cm³
2. Sebuah kerucut memiliki jari-jari alas 10 cm dan panjang garis pelukisnya 20 cm. Hitunglah berapa luas permukaan kerucut tersebut!
penyelesaian:
L = πr² + πrs
L = (3,14 × 10²) + (3,14 × 10 × 20)
L = 314 + 628
L = 942 cm²
Demikianlah pembahasan mengenai pengertian kerucut, ciri-ciri kerucut, bagian-bagian kerucut dan rumus-rumus kerucut beserta contoh soalnya. Semoga bermanfaat.
Baca Juga :