Contoh Soal Unsur-Unsur Lingkaran – Pada artikel ini akan dibahas contoh soal matematika tentang unsur-unsur lingkaran. Soal-soal telah dilengkapi dengan jawaban dan cara penyelesaiannya, sehingga diharapkan dapat lebih mudah dipahami.
Sebelum membahas contoh soal lingkaran, perlu diketahui bahwa lingkaran merupakan bangun datar yang memiliki unsur-unsur seperti jari-jari, diameter, busur, tali busur, juring, dan tembereng.
Untuk memahami unsur-unsur lingkaran, silahkan pelajari pada pembahasan unsur-unsur lingkaran. Nah, jika sudah dipahami dengan baik, silahlah simak contoh soal tentang unsur-unsur lingkaran berikut ini.
Contoh Soal Unsur-Unsur Lingkaran
A. Pilihlah jawaban yang benar pada soal-soal berikut ini!
1. Perhatikan gambar lingkaran di bawah ini!
Unsur lingkaran yang ditunjukan oleh garis OA dinamakan …..
a. jari-jari
b. diameter
c. busur
d. tali busur
Jawaban: a
2. Perhatikan gambar unsur lingkaran berikut ini!
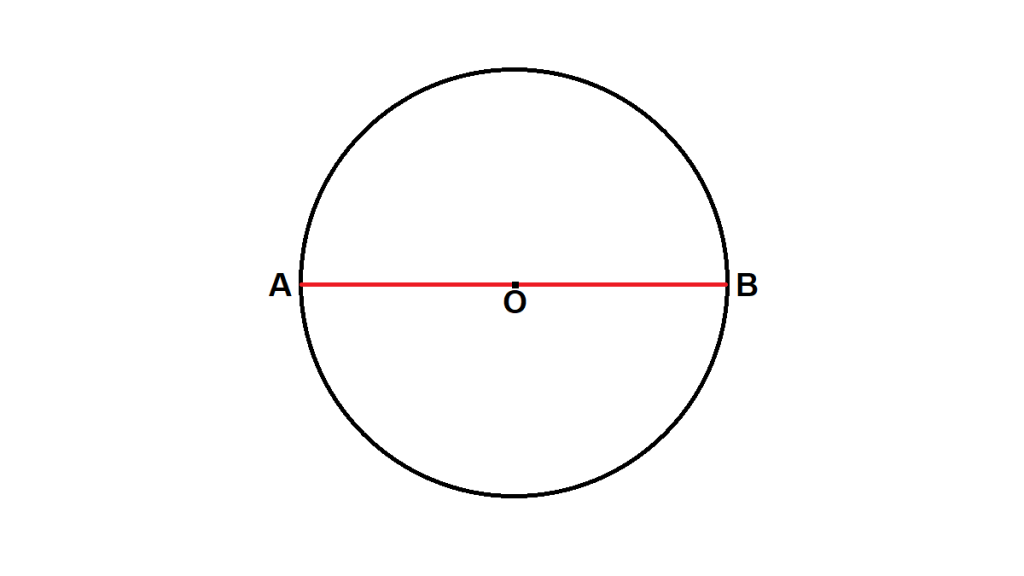
Unsur lingkaran yang ditunjukan oleh garis AB dinamakan …..
a. jari-jari
b. diameter
c. busur
d. tali busur
Jawaban: b
3. Pernyataan berikut ini yang benar mengenai hubungan antara jari-jari dan diameter adalah …..
a. r = d
b. r = 2 x d
c. d = 2 x r
d. d = 1/2 x r
Jawaban: c
4. Perhatikan gambar unsur lingkaran di bawah ini!
Garis lengkung BC merupakan unsur lingkaran yang disebut dengan …..
a. jari-jari
b. diameter
c. busur
d. tali busur
Jawaban: c
5. Perhatikan gambar unsur lingkaran berikut ini!
Garis lurus BC adalah unsur lingkaran yang dinamakan …..
a. juring
b. tembereng
c. busur
d. tali busur
Jawaban: d
6. Perhatikan gambar lingkaran di bawah ini!
Unsur lingkaran yang dibatasi oleh jari-jari OC dan jari-jari OD serta busur CD disebut …..
a. busur
b. tali busur
c. juring
d. tembereng
Jawaban: c
7. Perhatikan unsur lingkaran berikut ini!
Daerah yang dibatasi oleh busur BC dan tali busur BC pada lingkaran di atas dinamakan …..
a. tali busur
b. apotema
c. juring
d. tembereng
Jawaban: d
8. Perhatikan gambar lingkaran di bawah ini!
Garis OD merupakan unsur lingkaran yang disebut dengan …..
a. tali busur
b. apotema
c. juring
d. tembereng
Jawaban: b
9. Perhatikan gambar unsur lingkaran di bawah ini!
Garis lengkung yang dimulai dari titik A dan berakhir juga di titik A disebut …..
a. keliling
b. luas
c. apotema
d. tembereng
Jawaban: a
10. Perhatikan gambar lingkaran berikut ini!
Daerah yang diarsir pada gambar lingkaran di atas disebut …..
a. keliling
b. luas
c. apotema
d. tembereng
Jawaban: b
11. Perhatikan gambar unsur-unsur lingkaran berikut ini!
Unsur lingkaran yang disebut dengan sudut pusat yaitu …..
a. sudut BAD
b. sudut AOC
c. sudut ADB
d. sudut OBC
Jawaban: b
12. Perhatikan gambar unsur-unsur lingkaran di bawah ini!
Unsur lingkaran yang disebut dengan sudut keliling ditunjukan oleh …..
a. sudut BAD
b. sudut AOC
c. sudut ADB
d. sudut OBC
Jawaban: a
B. Soal Uraian
1. Perhatikan gambar unsur-unsur lingkaran di bawah ini!
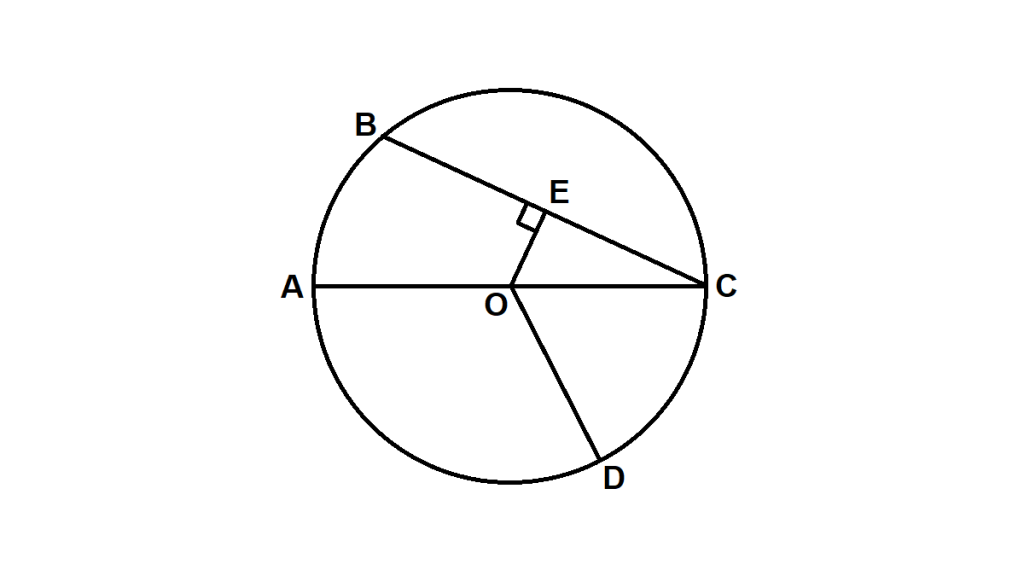
Tentukan unsur-unsur lingkaran berikut ini:
a. Titik pusat
b. Jari-Jari
c. Diameter
d. Busur
e. Tali Busur
f. Juring
g. Tembereng
h. Apotema
I. Sudut pusat
j. Sudut keliling
Penyelesaian:
a. Titik pusat = titik O
b. Jari-Jari = garis OA, OC, OD
c. Diameter = garis AC
d. Busur = garis lengkung AB, BC, CD, DA
e. Tali Busur = garis BC
f. Juring = Daerah yang dibatasi oleh COD
g. Tembereng = Daerah yang dibatasi oleh garis BC dan garis lengkung BC
h. Apotema = garis OE
I. Sudut pusat = sudut COD
j. Sudut keliling = sudut ACB
2. Perhatikan gambar lingkaran berikut ini!
Berapakah panjang apotema OE jika jari-jari lingkaran 10 cm dan tali busur BC adalah 12 cm?
Penyelesaian:
Perhatikan segitiga COE! segitiga tersebut merupakan segitiga siku-siku. Jadi untuk mencari apotema OE, kita dapat menggunakan rumus pythagoras!
OC² = CE² + OE²
OE² = OC² – CE²
OE = √OC² – CE²
CE = BC : 2
CE = 12 : 2
CE = 6 cm
OE = √10² – 6²
OE = √100 – 36
OE = √64
OE = 8 cm
Jadi, panjang apotema OE adalah 8 cm.
3. Perhatikan gambar lingkaran di bawah ini!
Jika besar sudut AOB = 90° dan jari OA = OB = 14 cm, Tentukanlah!
a. Keliling lingkaran
b. Luas Lingkaran
c. Luas juring lingkaran AOB
Penyelesaian:
a. K = 2 x π x r
K = 2 x 22/7 x 14
K = 88 cm
Jadi, keliling lingkaran adalah 88 cm
b. L = π x r²
L = 22/7 x 14²
L = 22/7 x 196
L = 616 cm²
Jadi, luas lingkaran adalah 616 cm².
c. Lj = (α/360°) x π x r²
Lj = (90°/360°) x 22/7 x 14²
Lj = 1/4 x 22/7 x 196
Lj = 1/4 x 616
Lj = 154 cm²
Jadi, luas juring lingkaran adalah 154 cm².
Demikianlah pembahasan mengenai contoh soal unsur-unsur lingkaran dan jawabannya. Semoga bermanfaat.
Baca Juga :
