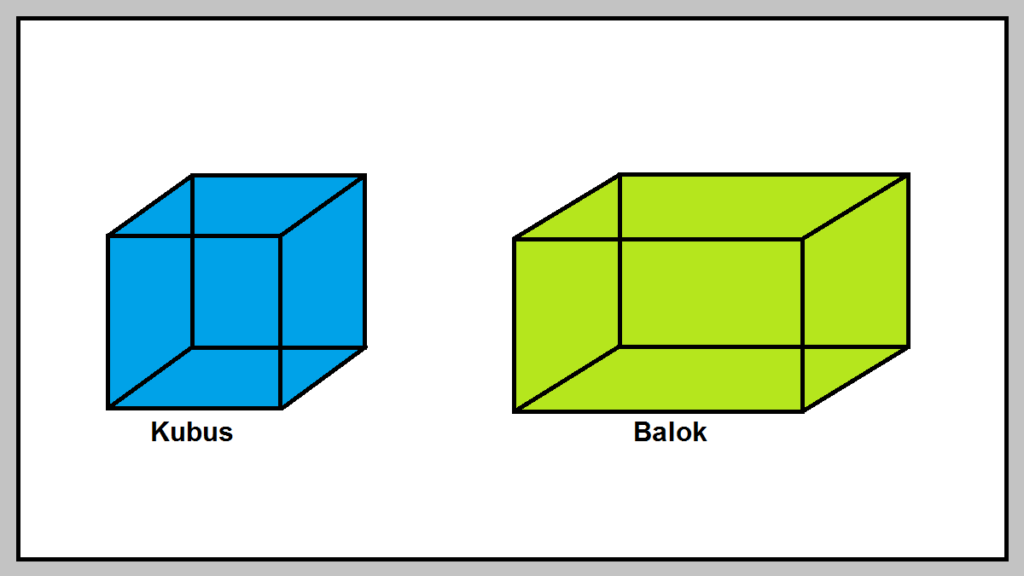
Kubus dan balok merupakan bangun ruang yang menarik untuk dipelajari. Kedua bangun ini sama-sama bangun ruang sisi datar, tetepi memiliki sifat yang berbeda. Pada artikel ini akan dijelaskan apa saja sifat-sifat kubus dan balok beserta rumusnya.
Kubus dan balok memiliki karakteristik berbeda. Perbedaannya yang paling mencolok terdapat pada bentuk sisinya. Sisi kubus semuanya berbentuk persegi, sedangkan sisi balok dapat berbentuk persegi dan persegi panjang.
Karena bentuk sisinya berbeda, rumus perhitungan volume kubus dan balok juga berbeda. Nah, untuk mengetahui apa saja sifat-sifat dan rumus-rumus kubus dan balok, silahkan simak pembahasan berikut ini.
Sifat-Sifat Kubus
Kubus adalah bangun ruang yang memiliki 6 sisi, 12 rusuk, dan 8 titik sudut. Sisi-sisi persegi berbentuk persegi. Untuk rusuknya juga semuanya berukuran sama panjang.
Untuk memahami bentuk kubus, perhatikan sifat-sifat kubusberikut ini:
- Memiliki 6 sisi
- Sisi-sisi kubus berbentuk persegi sama besar
- Memiliki 12 rusuk
- Rusuk-rusuk kubus memiliki ukuran sama panjang
- Memiliki 8 titik sudut
- Kubus memiliki 12 diagonal bidang
- Kubus memiliki 4 diagonal ruang
- Kubus memiliki 6 bidang diagonal
Sebagai bangun ruang, kubus memiliki perhitungan volume dan luas permukaan. Berikut adalah rumus-rumus untuk menghitung kubus:
| V = s x s x s |
| L = 6 x s x s |
Keterangan:
V = volume kubus
L = luas permukaan kubus
s = rusuk kubus
Contoh
Sebuah kubus memiliki panjang rusuk 5 cm. Tentukan volume dan luas permukaannya?
Penyelesaian:
V = s x s x s
V = 5 x 5 x 5
V = 125 cm³
Jadi, volume kubus adalah 125 cm³.
L = 6 x s x s
L = 6 x 5 x 5
L = 150 cm²
Jadi, luas permukaan kubus adalah 150 cm².
Sifat-Sifat Balok
Balok adalah bangun ruang yang dibatasi oleh 6 sisi, 12 rusuk, dan 8 titik sudut. Berbeda dengan kubus, sisi balok dapat berbentuk persegi dan persegi panjang, dengan setidaknya memiliki dua pasang sisi berukuran sama.
Berikut merupakan sifat-sifat yang dimiliki balok:
- Memiliki 6 sisi
- Sisi-sisi balok berbentuk persegi dan persegi panjang
- Sisi-sisi balok yang berhadapan sama besar
- Memiliki 12 rusuk
- Rusuk balok memiliki dimensi panjang, lebar, dan tinggi
- Memiliki 8 titik sudut
- Memiliki 12 diagonal bidang
- Memiliki 4 diagonal ruang
- Memiliki 6 bidang diagonal
Sama halnya dengan kubus, balok juga memiliki rumus volume dan luas permukaan. Adapun rumus-rumusnya yaitu sebagai berikut:
| V = p x l x t |
| L = 2 (p x l + l x t + p x t) |
Keterangan:
V = volume balok
L = luas permukaan balok
p = panjang
l = lebar
t = tinggi
Contoh
Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 5 cm. Berapakah volume dan luas permukaan balok?
Penyelesaian:
V = p x l x t
V = 10 x 6 x 5
V = 300 cm³
Jadi, volume balok adalah 300 cm³.
L = 2 (p x l + l x t + p x t)
L = 2 (10 x 6 + 6 x 5 + 10 x 5)
L = 2 (60 + 30 + 50)
L = 2 x 140
L = 280 cm²
Jadi, luas permukaan balok adalah 280 cm².
Demikianlah pembahasan mengenai sifat-sifat kubus dan balok beserta rumusnya. Semoga bermanfaat.
Baca Juga :