Pengertian Himpunan Dan Jenis-Jenis Operasi Himpunan – Himpunan adalah kumpulan dari beberapa objek yang dapat didefinisikan dengan jelas. Dalam matematika, terdapat beberapa jenis operasi himpunan, diantaranya yaitu gabungan, irisan, selisih, komplemen, dan beda setangkup.
Gabungan dari dua himpunan atau lebih ini dapat dioperasikan dan menghasilkan himpunan baru melalui konsep operasi himpunan. Agar jelas dalam memahami apa yang dimaksud dengan himpunan, berikut akan dibahas tentang pengertian himpunan dan jenis-jenis operasi himpunan.
Pengertian Himpunan
Himpunan adalah kumpulan dari suatu objek atau benda tertentu yang memiliki definisi yang jelas dan dapat dinyatakan sebagai satu kesatuan. Agar lebih dalam mudah memahami pengertian himpunan, perhatikan contoh himpunan berikut:
1. Himpunan bilangan asli
2. Himpunan bunga yang indah
Dari kedua contoh himpunan tersebut, kita dapat membedakan mana yang termasuk himpunan dan mana yang bukan himpunan. Berikut penjelasannya.
Himpunan bilangan asli termasuk dalam suatu himpunan, karena memiliki kumpulan bilangan yang dapat didefinisikan dengan jelas. Kita tahu bahwa himpunan bilangan asli dimulai dari angka satu, yakni 1, 2, 3, 4, dan seterusnya. Jika dimulai dari angka 0, maka bilangan tersebut bukan himpunan bilangan asli, melainkan himpunan bilangan cacah.
Sedangkan himpunan bunga yang indah bukan termasuk himpunan, karena tidak memiliki definisi yang jelas. Kata indah memiliki pengertian yang berbeda untuk setiap orang. Misalnya kita menganggap bunga A indah, tetapi belum tentu orang lain mengganggap bunga A indah. Oleh sebab itu, bunga yang indah bukan merupakan suatu himpunan.
Bagaimana Cara Menyatakan Himpunan?
Suatu himpunan dapat dinyatakan atau disimbolkan dengan huruf kapital. Jika anggota suatu himpunan berupa huruf, maka anggotanya dituliskan menggunakan huruf kecil. Berikut merupakan beberapa cara untuk menyatakan suatu himpunan.
1. Menggunakan Kata-Kata
Untuk menyatakan suatu himpunan, kita bisa menggunakan kata-kata, yaitu dengan menyebutkan semua definisi dari anggota himpunan tersebut di dalam kurung kurawal.
Contoh:
A merupakan bilangan bulat antara 5 dan 10. Untuk menyatakan himpunan A dengan kata-kata dituliskan menjadi :
A = {bilangan bulat antara 5 dan 10}
2. Menggunakan Notasi Pembentuk Himpunan
Cara untuk menyatakan suatu himpunan juga dapat menggunakan notasi pembentuk himpunan, yaitu dengan menyebutkan semua definisi dari anggota himpunan tersebut dalam suatu variabel yang dituliskan di dalam kurung kurawal.
Contoh:
A merupakan bilangan bulat antara 5 dan 10. Untuk menyatakan himpunan A dengan notasi pembentuk himpunan menjadi :
A= {x | 5 < x < 10, x ϵ bilangan bulat}
3. Dengan Mendaftarkan Seluruh Anggotanya
Cara untuk menyatakan himpunan selanjutnya yaitu dengan mendaftarkan atau menuliskan seluruh anggota dari himpunan tersebut di dalam kurung kurawal.
Contoh:
A merupakan bilangan bulat antara 5 dan 10. Untuk menyatakan himpunan A dengan mendaftarkan seluruh anggotanya menjadi :
A = {6, 7, 8, 9}
Jenis-Jenis Himpunan
Setelah memahami pengertian dan cara menyatakan suatu himpunan, berikut akan dijelaskan mengenai macam-macam himpunan. Secara umum, himpunan terdiri dari tiga jenis, yaitu himpunan semesta, himpunan kosong, dan himpunan bagian.
1. Himpunan Semesta
Himpunan semesta adalah himpunan yang memuat seluruh anggota dari himpunan yang dinyatakan. Himpunan semesta disimbolkan dengan huruf S. Sebagai contoh, A = {3, 5, 7, 9, 11}, maka himpunan semesta yang mungkin untuk menyatakan himpunan tersebut adalah S = {bilangan asli} atau S = { bilangan ganjil } atau S = {bilangan cacah}. Tetapi kita tidak dapat menyatakannya sebagai S = {bilangan prima}, karena terdapat angka 9 yang bukan termasuk bilangan prima.
2. Himpunan Kosong
Himpunan kosong adalah himpunan yang tidak memiliki anggota. Simbol untuk himpunan kosong adalah Ø atau { }. Sebagai contoh, B adalah himpunan bilangan asli negatif. Karena tidak ada bilangan asli yang negatif, sehingga B merupakan himpunan kosong yang tindak memiliki anggota. Jika dituliskan B = Ø atau B = { }.
3. Himpunan Bagian
Himpunan bagian adalah himpunan yang tersusun dari anggota himpunan lainnya. Jika himpunan A merupakan himpunan bagian B, dan setiap anggota himpunan A juga anggota himpunan B, maka dituliskan A ⊂ B atau B ⊃ A.
Contoh:
A = {1, 2, 3}
B = {1, 2, 3, 4, 5}
Maka A ⊂ B atau B ⊃ A
Jika ada anggota himpunan A yang bukan anggota B, maka A bukan himpunan bagian dari B dan dituliskan A ⊄ B.
Contoh:
A = {1, 2, 3, 4, 5}
B = {4, 5, 6}
Maka A ⊄ B
Jenis-Jenis Operasi Himpunan

Operasi himpunan sering digambarkan dengan menggunakan diagram venn. Diagram venn adalah penyajian suatu himpunan dengan menggunakan lingkaran. Untuk himpunan semesta pada diagram venn disimbolkan dengan gambar segi empat kecil.
Dalam perhitungannya, terdapat beberapa jenis operasi himpunan, diantaranya yaitu gabungan, irisan, selisih, komplemen, dan beda setangkup . Berikut pembahasannya.
1. Gabungan
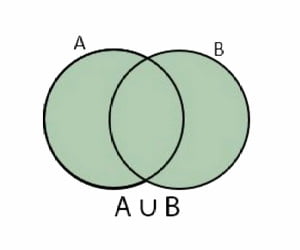
Operasi himpunan yang pertama adalah gabungan. Gabungan dari dua himpunan A dan himpunan B adalah himpunan yang terdiri dari semua anggota himpunan A dan himpunan B, dimana anggota yang sama hanya dituliskan satu kali. Himpunan A gabungan himpunan B dituliskan A ∪ B = {x | x ∈ A atau x ∈ B}
Contoh:
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
A ∪ B = {1, 2, 3, 4, 5, 6}
2. Irisan

Operasi himpunan yang kedua adalah irisan. Irisan dari himpunan A dan himpunan B adalah himpunan yang sama dari seluruh anggota himpunan A dan himpunan B. Dengan kata lain, suatu himpunan yang anggotanya ada di kedua himpunan tersebut. Himpunan A irisan himpunan B dituliskan A ∩ B = {x | x ∈ A dan x ∈ B}
Contoh:
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
A ∩ B = {3, 4}
3. Selisih

Operasi himpunan yang ketiga adalah selisih. Selisih dari himpunan A dan himpunan B adalah himpunan dari seluruh anggota himpunan A, tetapi tidak dimiliki oleh anggota himpunan B. Himpunan A selisih himpunan B dituliskan A-B = {x | x ∈ A atau x Ï B}
Contoh:
A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A-B = { 1, 4 }
4. Komplemen

Operasi himpunan yang keempat adalah komplemen. Komplemen dari himpunan A adalah himpunan seluruh elemen dari S yang tidak ada pada himpunan A. Komplemen himpunan A ditulis A1 atau Ac = {x | x ∈ S atau x Ï A}
Contoh:
A = {1, 2, … , 5}
S = {bilangan asli kurang dari 10}
Ac = {6, 7, 8, 9}
5. Beda Setangkup

Operasi himpunan yang kelima adalah beda setangkup. Beda setangkup dari himpunan A dan himpunan B akan menghasilkan suatu himpunan yang anggotanya ada pada himpunan A atau himpunan B, tetapi tidak pada keduanya. Beda setangkup himpunan A dan himpuna dituliskan A ⊕ B = {x | x ∈ A tetapi x ∉ B dan x ∈ B tetapi x ∉ A}
Contoh:
A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A ⊕ B = {1, 4, 7, 11}
Demikianlah pembahasan mengenai pengertian himpunan dan jenis-jenis operasi himpunan. Semoga bermanfaat.
Baca Juga :