Selain volume, tabung juga memiliki luas permukaan. Luas permukaan tabung merupakan jumlah total dari luas permukaannya. Nah, pada artikel ini akan dibahas tentang rumus untuk menghitung luas permukaan tabung dan contoh soalnya.
Tabung adalah bangun ruang yang dibatasi oleh 3 sisi, yaitu sisi alas, sisi atas, dan sisi selimut. Sisi alas dan sisi atasnya berbentuk lingkaran. Sedangkan sisi selimutnya berbentuk lengkungan persegi panjang. Luas sisi alas ditambah luas sisi atas ditambah luas selimut itulah yang dinamakan luas permukaan tabung.
Untuk mencari luas permukaan tabung, kita perlu memahami unsur-unsur yang berkaitan dengan perhitungan luas permukaan. Adapun unsur-unsur tersebut yaitu sebagai berikut:
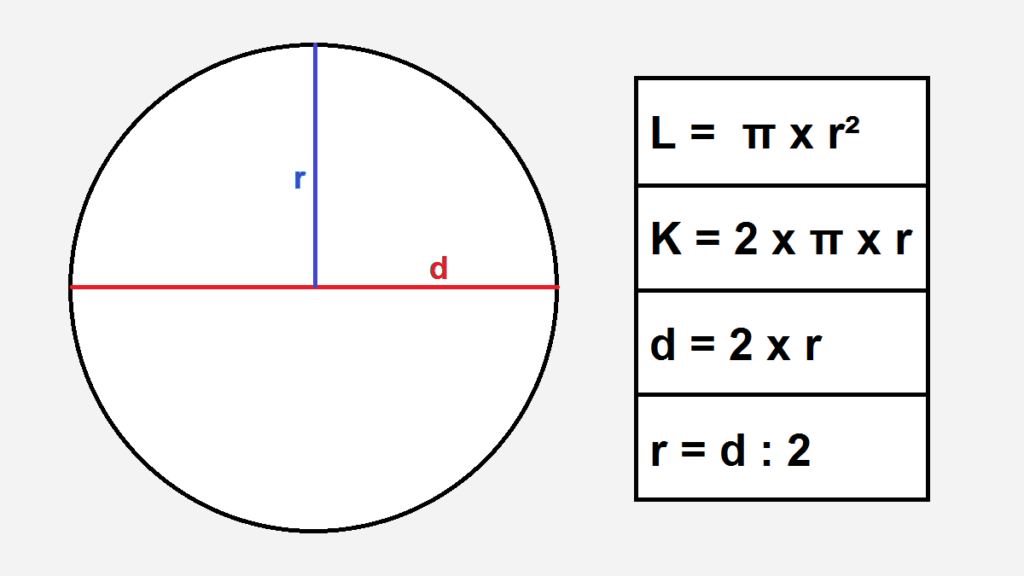
1. Jari-Jari Tabung (r)
Sisi alas dan sisi atas (tutup tabung) memiliki berentuk lingkaran. Jari-jari tabung adalah jari-jari yang terletak pada sisi alas atau sisi atasnya.
2. Tinggi Tabung (t)
Tinggi tabung adalah jarak antara sisi alas dan sisi atasnya. Tinggi tabung juga merupakan lebar dari sisi selimut tabung.
3. Selimut Tabung (Ls)
Selimut tabung adalah sisi tengah yang menghubungkan sisi alas dan sisi atas tabung. Selimut tabung berbentuk persegi panjang yang ukuran panjangnya sama dengan keliling sisi lingkaran tabung.
Rumus Luas Permukaan Tabung
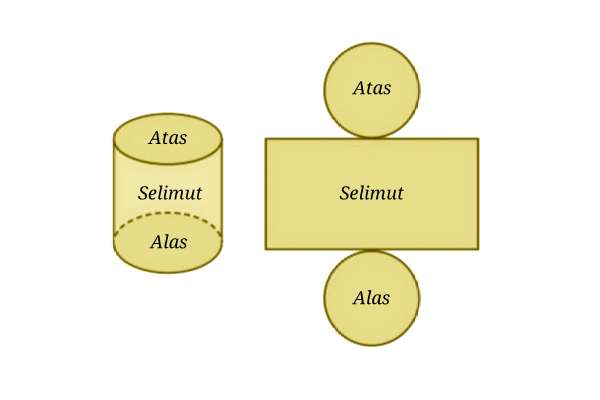
Perhatikan gambar di atas, jika sebuah tabung dibuka, maka akan diperoleh 2 sisi berbentuk lingkaran, serta 1 sisi berbentuk persegi panjang. Rumus luas sisi-sisi tabung dapat ditulis sebagai berikut:
- Luas alas tabung= π x r²
- Luas tutup tabung = π x r²
- Luas selimut tabung= (2 x π x r) x t
- Luas permukaan tabung = luas alas + luas atas + luas selimut
- Luas permukaan tabung = π x r² + π x r² + (2 x π x r) x t
- Luas permukaan tabung = 2 x π x r x (r + t)
Jadi, rumus untuk menghitung luas permukaan tabung adalah:
| LP = 2 x π x r x (r + t) |
Keterangan:
LP = luas permukaan tabung
π = 22/7 atau 3,14
r = jari-jari tabung
t = tinggi tabung
Contoh Soal
Berikut adalah contoh soal menghitung luas permukaan tabung dan cara penyelesaiannya.
1. Diketahui sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Berapakah luas permukaan tabung tersebut?
Penyelesaian:
LP = 2 x π x r x (r + t)
LP = 2 x 22/7 x 7 x (7 + 10)
LP = 2 x 22 x 17
LP = 748 cm²
Jadi, luas permukaan tabung tersebut adalah 748 cm².
2. Sebuah tabung memiliki jari-jari 14 cm dan tinggi 20 cm. Berapakah luas permukaan tabung?
Penyelesaian:
LP = 2 x π x r x (r + t)
LP = 2 x 22/7 x 14 x (14 + 20)
LP = 2 x 44 x 34
LP = 2.992 cm²
Jadi, luas permukaan tabung adalah 2.992 cm².
3. Berapakah luas perkukaan tabung yang memiliki jari-jari 10 cm dan tinggi 25 cm?
Penyelesaian:
LP = 2 x π x r x (r + t)
LP = 2 x 3,14 x 10 x (10 + 25)
LP = 2 x 31,4 x 35
LP = 2.198 cm²
Jadi, luas permukaan tabung adalah 2.198 cm².
Demikianlah pembahasan mengenai rumus luas permukaan tabung dan contoh soalnya. Semoga bermanfaat.
Baca Juga :