Belah Ketupat – Ketika lebaran, makanan paling populer yaitu ketupat. Bentuk ketupat merupakan salah satu contoh benda yang menyerupai belah ketupat. Apa itu belah ketupat?
Nah, untuk memahaminya, pada artikel ini akan dibahas secara lengkap mengenai pengertian, sifat-sifat, rumus luas dan keliling, beserta contoh soal belah ketupat.
Pengertian Belah Ketupat
Belah ketupat adalah bangun datar yang memiliki 4 sisi yang sama panjang, serta memiliki dua pasang sudut sama besar, yakni pasangan sudut lancip dan sudut tumpul.
Jika diperhatikan, persegi dan belah ketupat sama-sama memiliki empat sisi sama panjang. Namun sudut belah ketupat tidak berbentuk siku-siku. Jadi, belah ketupat berbeda dengan persegi.
Dalam kehidupan sehari-hari, terdapat beberapa benda yang menyerupai bentuk belah ketupat, diantaranya yaitu ketupat lebaran, bentuk kue lapis, dan variasi bentuk ventilasi.
Sifat-Sifat Belah Ketupat
Perhatikan gambar belah ketupat ABCD di bawah ini!
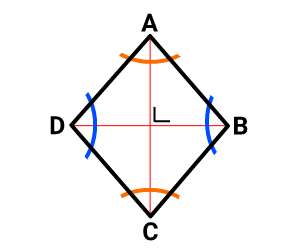
Belah ketupat memiliki ciri-ciri dan sifat-sifat sebagai berikut:
- Mempunyai 4 sisi sama panjang, sisi AB = BC = CD = DA
- Mempunyai 4 sudut, ∠ A, ∠ B, ∠ C dan ∠ D
- Sudut yang berhadapan sama besar, ∠ A = ∠ C dan ∠ B = ∠ D
- Mempunyai 2 sudut lancip, ∠ A = ∠ C = sudut lancip
- Mempunyai 2 sudut tumpul, ∠ B = ∠ D = sudut tumpul
- Mempunyai 2 garis diagonal, garis AC dan BD
- Kedua garis diagonalnya berpotongan tegak lurus
- Mempunyai 2 sumbu simetri
- Mempunyai 2 simetri lipat
- Mempunyai 2 simetri putar
Rumus Luas Belah Ketupat
Luas belah ketupat merupakan seberapa besar daerah yang dibatasi oleh sisi-sisinya. Rumus untuk menghitung luas belah ketupat adalah:
| L = 1/2 x d1 x d2 |
Keterangan:
L = luas
d1 = diagonal 1
d2 = diagonal 2
Rumus Keliling Belah Ketupat
Keliling belah ketupat merupakan jumlah seluruh ukuran sisinya. Rumus untuk menghitung keliling belah ketupat adalah sebagai berikut:
| K = 4 x s |
Keterangan:
K = keliling
s = sisi
Contoh Soal Belah Ketupat
1. Sebutkan 5 ciri-ciri belah ketupat!
Penyelesaian:
- Mempunyai 4 sisi sama panjang
- Mempunyai 4 sudut
- Mempunyai 2 garis diagonal
- Mempunyai 2 simetri lipat
- Mempunyai 2 simetri putar
2. Sebuah belah ketupat memiliki panjang diagonal 10 cm dan 20 cm. Hitunglah luas belah ketupat tersebut!
Penyelesaian:
L = 1/2 x d1 x d2
L = 1/2 x 10 x 20
L = 1/2 x 200
L = 100 cm²
Jadi, luas belah ketupat tersebut adalah 100 cm²
3. Belah ketupat memiliki ukuran sisi 5 cm. Berapakah keliling belah ketupat tersebut?
Penyelesaian:
K = 4 x s
K = 4 x 5
K = 20 cm
Jadi, keliling belah ketupat tersebut adalah 20 cm.
4. Keliling belah ketupat adalah 40 cm. berapakah panjang sisi belah ketupat?
Penyelesaian:
s = K : 4
s = 40 : 4
s = 10 cm
Jadi, sisi belah ketupat tersebut adalah 10 cm.
5. Luas belah ketupat adalah 20 cm². Jika panjang diagonal pertama 5 cm, berapakah panjang diagonal lainnya?
Penyelesaian:
d2 = (2 x L) : d1
d2 = (2 x 20) : 5
d2 = 40 : 5
d2 = 8 cm
Jadi, diagonal belah ketupat lainnya adalah 8 cm.
Demikianlah pembahasan mengenai pengertian, sifat-sifat, rumus luas dan keliling, serta contoh soal belah ketupat. Semoga bermanfaat.
Baca Juga :