Rumus Luas Permukaan Balok – Balok merupakan salah satu jenis bangun ruang. Setiap bangun ruang memiliki luas permukaan. Nah, pada kesempatan kali ini akan dibahas tentang rumus luas permukaan balok dan contoh soalnya.
Balok adalah bangun ruang yang dibatasi oleh enam sisi berbentuk segi empat. Sisi balok dapat berbentuk persegi dan persegi panjang. Dengan begitu, luas permukaan balok dapat dihitung dengan cara menjumlahkan seluruh luas sisi balok dengan menghitung luas persegi atau persegi panjang.
Nah, bagi yang belum paham bagaimana cara menghitung luas permukaan balok, silahkan simak pembahasan berikut ini mengenai rumus yang digunakan untuk menghitung luas permukaan balok dan contoh soalnya.
Rumus Luas Permukaan Balok
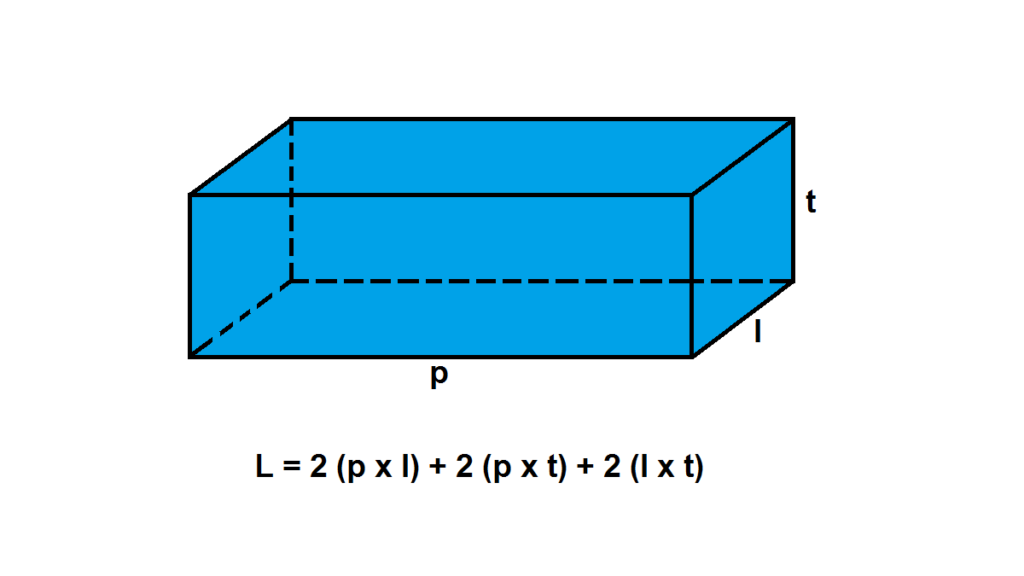
Luas permukaan balok adalah luas seluruh sisi balok. Luas permukaan balok dapat dihitung dengan cara menjumlahkan seluruh sisi balok. Perhatikan gambar di bawah ini!
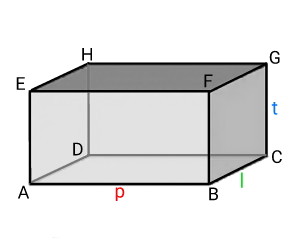
Sisi-sisi balok pada gambar di atas ditunjukan oleh:
- Sisi atas (EFGH)
- Sisi bawah/alas (ABCD)
- Sisi kanan (BCGF)
- Sisi kiri (ADHE)
- Sisi depan (ABFE)
- Sisi belakang (DCGH)
Jika rusuk panjang balok dituliskan = p, rusuk lebar balok = l, dan rusuk tinggi balok = t, maka diperoleh rumus-rumus luas sisi balok sebagai berikut:
- Luas Sisi Alas Balok = p x l
- Luas Sisi Depan = p x t
- Luas Sisi Samping = l x t
Dari rumus-rumus tersebut, maka diperoleh rumus untuk menghitung luas permukaan balok adalah sebagai berikut:
| Lp = 2 (p x l + p x t + l x t) |
Keterangan:
Lp = luas permukaan balok
p = panjang balok
l = lebar balok
t = tinggi balok
Satuan luas = satuan panjang persegi, misalnya m², cm², dan lain-lain.
Contoh Soal Luas Permukaan Balok
Untuk memudahkan dalam memahami perhitungan luas permukaan balok, silahkan simak contoh soal berikut ini.
1. Sebuah balok memiliki ukuran panjang 10 cm, lebar 6 cm, tinggi 5 cm. Berapakah luas permukaan balok tersebut?
Penyelesaian:
Lp = 2 x (p x l + p x t + l x t)
Lp = 2 x (10 x 6 + 10 x 5 + 6 x 5)
Lp = 2 x (60 + 50 + 30)
Lp = 2 x 140
Lp = 280 cm²
Jadi, luas permukaan balok tersebut adalah 280 cm².
2. Sebuah balok mempunyai panjang 20 cm, lebar 10 cm, dan tinggi 5 cm. Hitunglah berapa luas permukaan balok tersebut!
Penyelesaian:
Lp = 2 x (p x l + p x t + l x t)
Lp = 2 x (20 x 10 + 20 x 5 + 10 x 5)
Lp = 2 x (200 + 100 + 50)
Lp = 2 x 350
Lp = 700 cm²
Jadi, luas permukaan balok tersebut adalah 700 cm².
3. Diketahui luas permukaan sebuah balok adalah 348 cm². Jika diketahui
lebar balok 6 cm dan tinggi 4cm, hitunglah berapa panjang balok tersebut!
Penyelesaian:
Lp = 2 x (p x l + p x t + l x t)
348 = 2 x (p x 6 + p x 4 + 6 x 4)
348 = 2 x (6p + 4p + 24)
348 = 2 x (10p + 24)
348 = (2 x 10p) + (2 x 24)
348 = 20p + 48
348 – 48 = 20p
20p = 300
p = 300 : 20
p = 15 cm
Jadi, panjang balok tersebut adalah 15 cm.
4. Diketahui luas permukaan sebuah balok adalah 220 cm². Jika diketahui
panjang balok 10 cm dan tinggi 4 cm, hitunglah berapa lebar balok tersebut!
Penyelesaian:
Lp = 2 x (p x l + p x t + l x t)
220 = 2 x (10 x l + l x 4 + 10 x 4)
220 = 2 x (10l + 4l + 10 × 4)
220 = 2 x (14l + 40)
220 = (2 x 14l) + (2 x 40)
220 = 28l + 80
220 – 80 = 28l
140 = 28l
l = 140 : 28
l = 5 cm
Jadi, lebar balok tersebut adalah 5 cm.
5. Diketahui luas permukaan sebuah balok adalah 94 cm². Jika diketahui
panjang balok 5 cm dan lebar 4 cm, hitunglah berapa tinggi balok tersebut!
Penyelesaian:
Lp = 2 x (p x l + p x t + l x t)
94 = 2 x (5 × 4 + 4 x t + 5 x t)
94 = 2 x (20 + 4t + 5t)
94 = 2 x (20 + 9t)
94 = (2 x 20) + (2 x 9t)
94 = 40 + 18t
94 – 40 = 18t
54 = 18t
t = 54 : 18
t = 3 cm
Jadi, tinggi balok tersebut adalah 3 cm.
Demikianlah pembahasan mengenai rumus luas permukaan balok dan contoh soalnya. Semoga bermanfaat.
Baca Juga :