Rumus Perbandingan Senilai Dan Berbalik Nilai

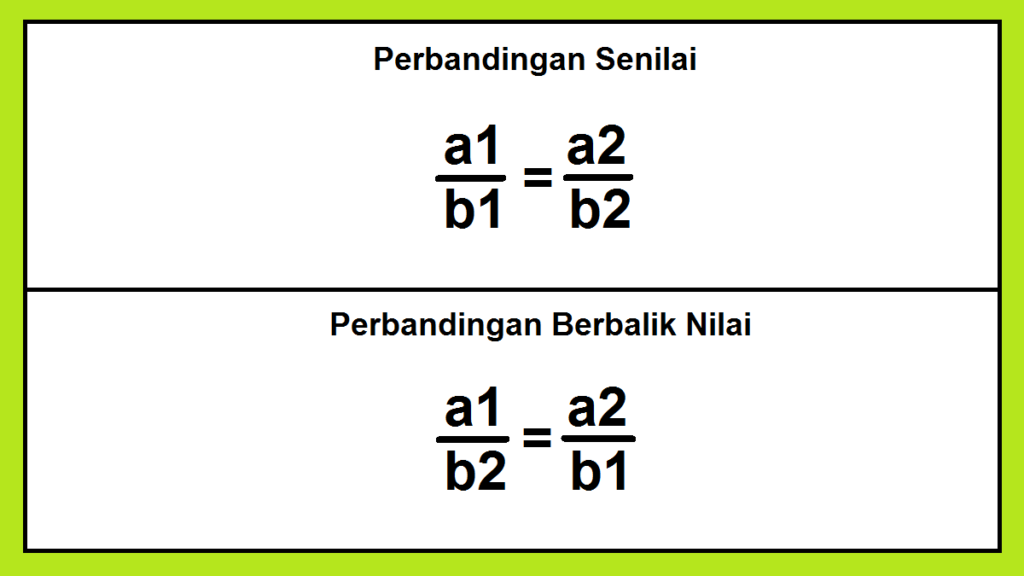
Rumus Perbandingan Senilai Dan Berbalik Nilai – Perbandingan merupakan rasio yang menyatakan persamaan atau perbedaan pada dua variabel. Dalam pelajaran matematika, setiap siswa wajib memahami rumus perbandingan senilai dan berbalik nilai.

Berikut akan dijelaskan bagaimana cara menghitung perbandingan senilai dan berbalik nilai beserta contoh soalnya.

Rumus Perbandingan Senilai

Perbandingan senilai adalah suatu perbandingan yang menyatakan jika nilai salah satu variabel bertambah, maka nilai variabel lainnya juga akan bertambah. Jika nilai salah satu variable menurun, maka nilai variable lainnya akan menurun.

Contoh perbandingan senilai dapat dilihat pada perbandingan jumlah dan harga suatu barang. Misalnya satu pensil harganya Rp 2.000, maka harga lima pensil adalah Rp 10.000.

Dari contoh tersebut, maka dapat ditentukan bahwa rumus untuk menghitung perbandingan senilai adalah:

a1/b1 = a2/b2

Contoh Soal

1. Harga 3 buku adalah Rp 6.000. Berapa harga 7 buku?

Penyelesaian:
a1/b1 = a2/b2
3/6.000 = 7/b2 (kalikan silang)
3 x b2 = 6.000 x 7
3 x b2 = 42.000
b2 = 42.000 : 3
b2 = 14.000
Jadi, harga 7 buku adalah Rp 14.000.

Baca Lainnya : Cara Menghitung Nilai Rata-Rata Dengan Mudah

2. Sebuah toko kue dapat membuat 400 kue dalam 8 hari. Berapa jumlah kue yang dapat dibuat toko kue selama 20 hari?

Penyelesaian:
a1/b1 = a2/b2
400/8 = a2/20 (kalikan silang)
400 x 20 = 8 x a2
8.000 = 8 x a2
a2 = 8.000 : 8
a2 = 1.000
Jadi, jumlah kue yang dapat dibuat selama 20 hari adalah 1.000.

Rumus Perbandingan Berbalik Nilai

Perbandingan berbalik nilai adalah suatu perbandingan yang menyatakan jika nilai salah satu variabel bertambah, maka nilai variabel lainnya akan berkurang.

Perhatikan contoh perbandingan berbalik nilai berikut ini, sebuah proyek pembangunan rumah dikerjakan oleh 10 orang memerlukan waktu 30 hari. Jika proyek tersebut dikerjakan 15 orang, maka akan selesai dalam 20 hari.

Dari contoh tersebut, maka rumus untuk menghitung perbandingan senilai adalah sebagai berikut:

a1/b2 = a2/b1

Contoh Soal

1. Kota A dan kota B ditempuh menggunakan mobil dengan kecepatan 60 km/jam dalam waktu 70 menit. Berapakah kecepatan mobil jika ditempuh dalam waktu 50 menit?

Baca Lainnya : Cara Menghitung Luas Permukaan Prisma Segitiga

Penyelesaian:
a1/b2 = a2/b1
60/50 = a2/70 (kalikan silang)
60 x 70 = 50 x a2
4.200 = 50 x a2
a2 = 4.200 : 50
a2 = 84
Jadi, jika ditempuh dalam waktu 50 menit, maka kecepatan mobil adalah 84 km/jam.

2. Sebuah persegi panjang memiliki ukuran panjang 20 cm dan lebar 10 cm. Jika ukuran panjang dibuat 25 cm, berapa ukuran lebarnya agar luas persegi panjang tetap?

Penyelesaian:
a1/b2 = a2/b1
20/b2 = 25/10
20 x 10 = b2 x 25
200 = b2 x 25
b2 = 200 : 25
b2 = 8
Jadi, ukuran lebar persegi panjang harus 8 cm.

Demikianlah pembahasan mengenai rumus untuk menghitung perbandingan senilai dan berbalik nilai. Semoga bermanfaat.

Baca Juga :