Cara Menghitung Volume Bangun Ruang Gabungan – Dalam materi bangun ruang, tentunya telah diajarkan rumus untuk menghitung volume. Untuk menentukan volume suatu bangun ruang mungkin bukan masalah yang sulit. Namun, bagaimana jika dalam soal terdapat perhitungan volume bangun ruang gabungan?
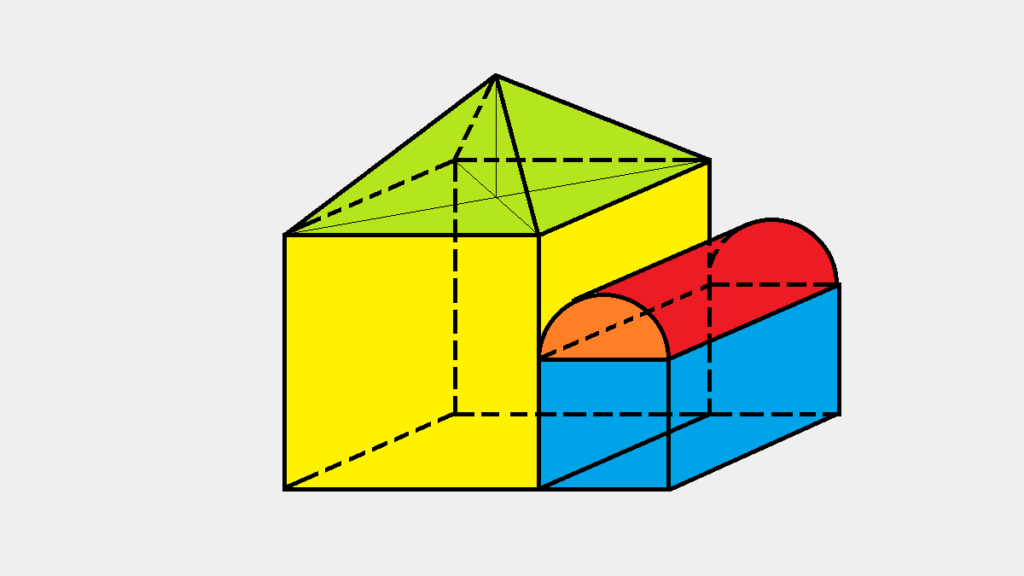
Bangun ruang gabungan adalah sebuah bangun yang terbentuk oleh beberapa bangun ruang. Contohnya seperti kubus dan limas, balok dan prisma, tabung dan kerucut, dan lain-lain. Lalu, bagaimanakah cara menghitung volume bangun ruang gabungan? Seperti apa rumus yang digunakan untuk menghitung volumenya?
Untuk menghitung volume gabungan bangun ruang sebenarnya caranya tidak begitu sulit. Yaitu dengan cara menjumlahkan seluruh volume masing-masing pada bangun pembentuknya. Nah, bagi yang masih bingung dalam mengerjakan soal tentang volume bangun ruang gabungan, silahkan simak pembahasan berikut ini.
Rumus Volume Bangun Ruang
Volume bangun ruang gabungan dapat ditentukan dari penjumlahan seluruh volume bangun pembentuknya. Untuk itu, dalam mengerjakan soal volume pada bangun ruang gabungan, kita perlu mengetahui rumus volume bangun ruang. Berikut merupakan rumus mencari volume bangun ruang.
| Volume Kubus = s x s x s |
| Volume Balok = p x l x t |
| Volume Limas = 1/3 x La x t |
| Volume Prisma = La x t |
| Volume Kerucut = 1/3 x π x r² x t |
| Volume Tabung = π x r² x t |
| Volume Boa = 4/3 x π x r³ |
Dengan rumus volume bangun ruang, maka memudahkan kita dalam menghitung volume bangun ruang gabungan.
Cara Menghitung Volume Bangun Ruang Gabungan
A. Volume Bangun Ruang Kubus Dan Balok
Penyelesaian:
Volume Kubus = s x s x s
Volume Kubus = 7 x 7 x 7
Volume Kubus = 343 cm³
Volume Balok = p x l x t
Volume Balok = 20 x 5 x 8
Volume Balok = 800 cm³
Volume bangun = volume kubus + volume balok
Volume bangun = 343 + 800 = 1.143 cm³
Jadi, volume bangun ruang gabungan dari kubus dan balok adalah 1.143 cm³.
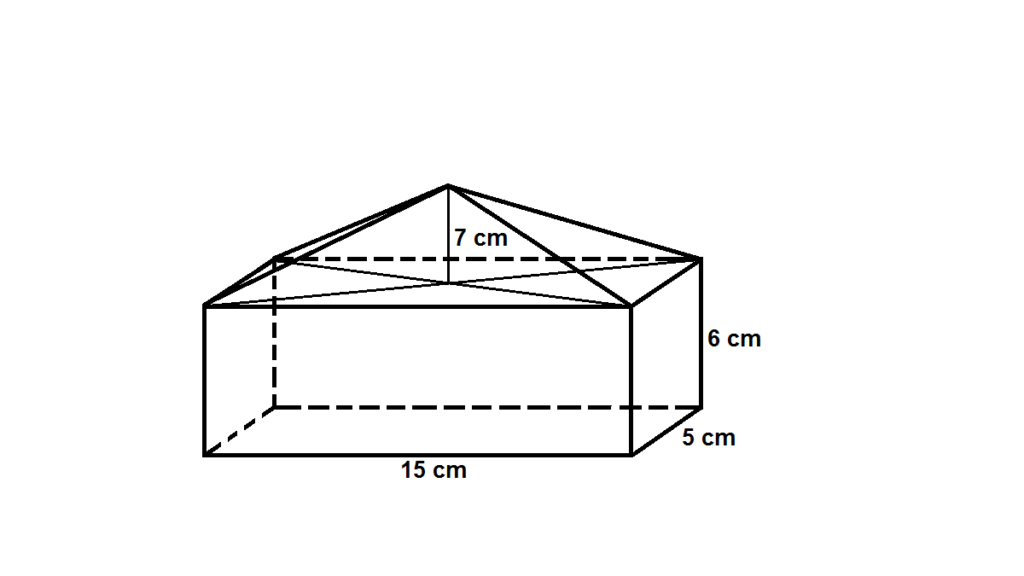
B. Volume Bangun Ruang Limas Dan Balok
Penyelesaian:
Volume Limas = 1/3 x La x t
Volume Limas = 1/3 x (p x l) x t
Volume Limas = 1/3 x (15 x 5) x 7
Volume Limas = 1/3 x 525
Volume Limas = 175 cm³
Volume Balok = p x l x t
Volume Balok = 15 x 5 x 6
Volume Balok = 450 cm³
Volume bangun = volume limas + volume balok
Volume bangun = 175 + 450 = 625 cm³
Jadi, volume bangun ruang gabungan dari kubus dan balok adalah 625 cm³.
C. Volume Bangun Ruang Prisma Dan Balok
Penyelesaian:
Volume Prisma = La x t
Volume Prisma = (1/2 x a x t) x t
Volume Prisma = (1/2 x 12 x 10) x 25
Volume Prisma = 60 x 25
Volume Prisma = 1.500 cm³
Volume Balok = p x l x t
Volume Balok = 25 x 12 x 15
Volume Balok = 4.500 cm³
Volume bangun = volume prisma + volume balok
Volume bangun = 1.500 + 4.500 = 6.000 cm³
Jadi, volume bangun ruang gabungan dari prisma dan balok adalah 6.000 cm³.
D. Volume Bangun Ruang Kerucut Dan Tabung
Penyelesaian:
Volume Kerucut = 1/3 x π x r² x t
Volume Kerucut = 1/3 x 22/7 x 7² x 10
Volume Kerucut = 1/3 x 1.540
Volume Kerucut = 513,33 cm³
Volume Tabung = π x r² x t
Volume Tabung = 22/7 x 7² x 15
Volume Tabung = 2.310 cm³
Volume bangun = volume kerucut + volume tabung
Volume bangun = 513,33 + 2.310 = 2.823,33 cm³
Jadi, volume bangun ruang gabungan dari kerucut dan tabung adalah 2.823,33 cm³.
E. Volume Bangun Ruang Kerucut Dan Setengah Bola
Penyelesaian:
Volume Kerucut = 1/3 x π x r² x t
Volume Kerucut = 1/3 x 22/7 x 7² x 8
Volume Kerucut = 1/3 x 1.232
Volume Kerucut = 410,67 cm³
Volume Setengah Bola = 1/2 x 4/3 x π x r³
Volume Setengah Bola = 2/3 x π x r³
Volume Setengah Bola = 2/3 x 22/7 x 7³
Volume Setengah Bola = 2/3 x 1.078
Volume Setengah Bola = 718,67 cm³
Volume bangun = volume kerucut + volume setengah bola
Volume bangun = 410,67 + 718,67 = 1.129,34 cm³
Jadi, volume bangun ruang gabungan dari kerucut dan setengah bola adalah 1.129,34 cm³.
F. Volume Bangun Ruang Balok Dan Setengah Tabung
Penyelesaian:
Volume Balok = p x l x t
Volume Balok = 25 x 10 x 8
Volume Balok = 2.000 cm³
Volume Setengah Tabung = 1/2 x π x r² x t
Volume Setengah Tabung = 1/2 x 3,14 x 5² x 25
Volume Setengah Tabung = 1/2 x 1.962,5
Volume Setengah Tabung = 981,25 cm³
Volume bangun = volume balok + volume setengah tabung
Volume bangun = 2.000 + 981,25 cm³
Jadi, volume bangun ruang gabungan dari balok dan setengah tabung adalah 2.981,25 cm³.
Demikianlah pembahasan mengenai cara menghitung volume bangun ruang gabungan dan contoh soalnya. Semoga bermanfaat.
Baca Juga :